Variables, Distributions and Summary Statistics

Today we learn how to describe data

Variables
Distributions
- Definition
- Graphical representation
- Common distributions
Central tendency
- Mean
- Median

Spread
- Range, quantiles, and the IQR
- Variance and standard deviation

A variable is …

Some measure that can vary.

Variables

Imagine you fill out a survey about your way to school.

Variables

Survey Question	Answer Options	Variable Name	Variable Type
How far do you live from the Jourdan University building?
How do you get there, usually?
How much time approximately does it take you to get there?
What arrondissement/suburb do you live in?
Compared to your classmates, how close do you think you live to University?
What’s the most annoying part of your itinerary to/from university?
Please indicate your level of (dis)agreement with the following statement: 'My itinerary to university is annoying.'

Variables

Survey Question	Answer Options	Variable Name	Variable Type
How far do you live from the Jourdan University building?	Use the exact distance in km
How do you get there, usually?	Bike, Metro, Walking, or Other
How much time approximately does it take you to get there?	less than 15 mins, between 15 and 60 mins, more than 60 mins
What arrondissement/suburb do you live in?	Open-ended
Compared to your classmates, how close do you think you live to University?	Closer, About the same, Further away
What’s the most annoying part of your itinerary to/from university?	Describe briefly
Please indicate your level of (dis)agreement with the following statement: 'My itinerary to university is annoying.'	1: Fully disagree – 5: Fully agree

Variables

Survey Question	Answer Options	Variable Name
How far do you live from the Jourdan University building?	Use the exact distance in km	Distance to school
How do you get there, usually?	Bike, Metro, Walking, or Other	Mode of transportation
How much time approximately does it take you to get there?	less than 15 mins, between 15 and 60 mins, more than 60 mins	Travel time
What arrondissement/suburb do you live in?	Open-ended	Place of residence
Compared to your classmates, how close do you think you live to University?	Closer, About the same, Further away	Relative perceived distance
What’s the most annoying part of your itinerary to/from university?	Describe briefly	Object of annoyance
Please indicate your level of (dis)agreement with the following statement: 'My itinerary to university is annoying.'	1: Fully disagree – 5: Fully agree	Degree of annoyance

Variables

Survey Question	Answer Options	Variable Name	Variable Type
How far do you live from the Jourdan University building?	Use the exact distance in km	Distance to school	Numeric
How do you get there, usually?	Bike, Metro, Walking, or Other	Mode of transportation
How much time approximately does it take you to get there?	less than 15 mins, between 15 and 60 mins, more than 60 mins	Travel time
What arrondissement/suburb do you live in?	Open-ended	Place of residence
Compared to your classmates, how close do you think you live to University?	Closer, About the same, Further away	Relative perceived distance
What’s the most annoying part of your itinerary to/from university?	Describe briefly	Object of annoyance
Please indicate your level of (dis)agreement with the following statement: 'My itinerary to university is annoying.'	1: Fully disagree – 5: Fully agree	Degree of annoyance

Variables

Survey Question	Answer Options	Variable Name	Variable Type
How far do you live from the Jourdan University building?	Use the exact distance in km	Distance to school	Numeric
How do you get there, usually?	Bike, Metro, Walking, or Other	Mode of transportation	Nominal
How much time approximately does it take you to get there?	less than 15 mins, between 15 and 60 mins, more than 60 mins	Travel time
What arrondissement/suburb do you live in?	Open-ended	Place of residence
Compared to your classmates, how close do you think you live to University?	Closer, About the same, Further away	Relative perceived distance
What’s the most annoying part of your itinerary to/from university?	Describe briefly	Object of annoyance
Please indicate your level of (dis)agreement with the following statement: 'My itinerary to university is annoying.'	1: Fully disagree – 5: Fully agree	Degree of annoyance

Variables

Survey Question	Answer Options	Variable Name	Variable Type
How far do you live from the Jourdan University building?	Use the exact distance in km	Distance to school	Numeric
How do you get there, usually?	Bike, Metro, Walking, or Other	Mode of transportation	Nominal
How much time approximately does it take you to get there?	less than 15 mins, between 15 and 60 mins, more than 60 mins	Travel time	Ordinal
What arrondissement/suburb do you live in?	Open-ended	Place of residence
Compared to your classmates, how close do you think you live to University?	Closer, About the same, Further away	Relative perceived distance
What’s the most annoying part of your itinerary to/from university?	Describe briefly	Object of annoyance
Please indicate your level of (dis)agreement with the following statement: 'My itinerary to university is annoying.'	1: Fully disagree – 5: Fully agree	Degree of annoyance

Variables

Survey Question	Answer Options	Variable Name	Variable Type
How far do you live from the Jourdan University building?	Use the exact distance in km	Distance to school	Numeric
How do you get there, usually?	Bike, Metro, Walking, or Other	Mode of transportation	Nominal
How much time approximately does it take you to get there?	less than 15 mins, between 15 and 60 mins, more than 60 mins	Travel time	Ordinal
What arrondissement/suburb do you live in?	Open-ended	Place of residence	Nominal
Compared to your classmates, how close do you think you live to University?	Closer, About the same, Further away	Relative perceived distance
What’s the most annoying part of your itinerary to/from university?	Describe briefly	Object of annoyance
Please indicate your level of (dis)agreement with the following statement: 'My itinerary to university is annoying.'	1: Fully disagree – 5: Fully agree	Degree of annoyance

Variables

Survey Question	Answer Options	Variable Name	Variable Type
How far do you live from the Jourdan University building?	Use the exact distance in km	Distance to school	Numeric
How do you get there, usually?	Bike, Metro, Walking, or Other	Mode of transportation	Nominal
How much time approximately does it take you to get there?	less than 15 mins, between 15 and 60 mins, more than 60 mins	Travel time	Ordinal
What arrondissement/suburb do you live in?	Open-ended	Place of residence	Nominal
Compared to your classmates, how close do you think you live to University?	Closer, About the same, Further away	Relative perceived distance	Ordinal
What’s the most annoying part of your itinerary to/from university?	Describe briefly	Object of annoyance
Please indicate your level of (dis)agreement with the following statement: 'My itinerary to university is annoying.'	1: Fully disagree – 5: Fully agree	Degree of annoyance

Variables

Survey Question	Answer Options	Variable Name	Variable Type
How far do you live from the Jourdan University building?	Use the exact distance in km	Distance to school	Numeric
How do you get there, usually?	Bike, Metro, Walking, or Other	Mode of transportation	Nominal
How much time approximately does it take you to get there?	less than 15 mins, between 15 and 60 mins, more than 60 mins	Travel time	Ordinal
What arrondissement/suburb do you live in?	Open-ended	Place of residence	Nominal
Compared to your classmates, how close do you think you live to University?	Closer, About the same, Further away	Relative perceived distance	Ordinal
What’s the most annoying part of your itinerary to/from university?	Describe briefly	Object of annoyance	Open-ended
Please indicate your level of (dis)agreement with the following statement: 'My itinerary to university is annoying.'	1: Fully disagree – 5: Fully agree	Degree of annoyance

Variables

Survey Question	Answer Options	Variable Name	Variable Type
How far do you live from the Jourdan University building?	Use the exact distance in km	Distance to school	Numeric
How do you get there, usually?	Bike, Metro, Walking, or Other	Mode of transportation	Nominal
How much time approximately does it take you to get there?	less than 15 mins, between 15 and 60 mins, more than 60 mins	Travel time	Ordinal
What arrondissement/suburb do you live in?	Open-ended	Place of residence	Nominal
Compared to your classmates, how close do you think you live to University?	Closer, About the same, Further away	Relative perceived distance	Ordinal
What’s the most annoying part of your itinerary to/from university?	Describe briefly	Object of annoyance	Open-ended
Please indicate your level of (dis)agreement with the following statement: 'My itinerary to university is annoying.'	1: Fully disagree – 5: Fully agree	Degree of annoyance	Ordinal/Numeric/Discrete

Overview Variable Types

Variable Type	Description	Example
Nominal	The color of a flower is another example of a nominal variable. Is the flower white, orange, or red? None of those options is “more” than the others; they’re just different.	Flower color (White, Orange, Red)
Ordinal	An ordinal variable, just like nominal variables, has categories. But some values are clearly “more” and others clearly “less” - you can ‘order’ observations. However, it is not clear how much more or less one value is than another, and differences might not always be the same between one value and the next.	Satisfaction levels (Low, Medium, High)
Continuous	A continuous variable can take any numeric value within a given range.	A person's height (e.g., 170.5 cm)
Discrete	A discrete variable is numeric, but can only take specific, distinct values. For example, the score given by a judge to a gymnast (only integer values between 0 and 10).	A judge's score in a gymnast competition (only integer values between 0 and 10)
Qualitative	Free text. To quantify it, people typically try to cateogrize them.	Open-ended survey answers (e.g. 'Describe your day in detail') or a data frame with news paper headlines

Distributions

The point of descriptive statistics is to summarize a big table of values with a small set of tractable statistics
The most comprehensive way to characterize a variable/vector is to compute its distribution:
- What are the values the variable takes?
- How frequently does each of these values appear?

Distributions

Consider this variable

We can count how many times each value appears

# A tibble: 8 × 2
     V1     n
  <int> <int>
1     1     1
2     2     1
3     3     2
4     4     4
5     5     5
6     6     9
7     7     6
8     8     2

Voilà the distribution of our variable.

Distributions

We can represent this distribution graphically with a bar plot.

Each possible value on the x-axis
Their number of occurrences on the y-axis

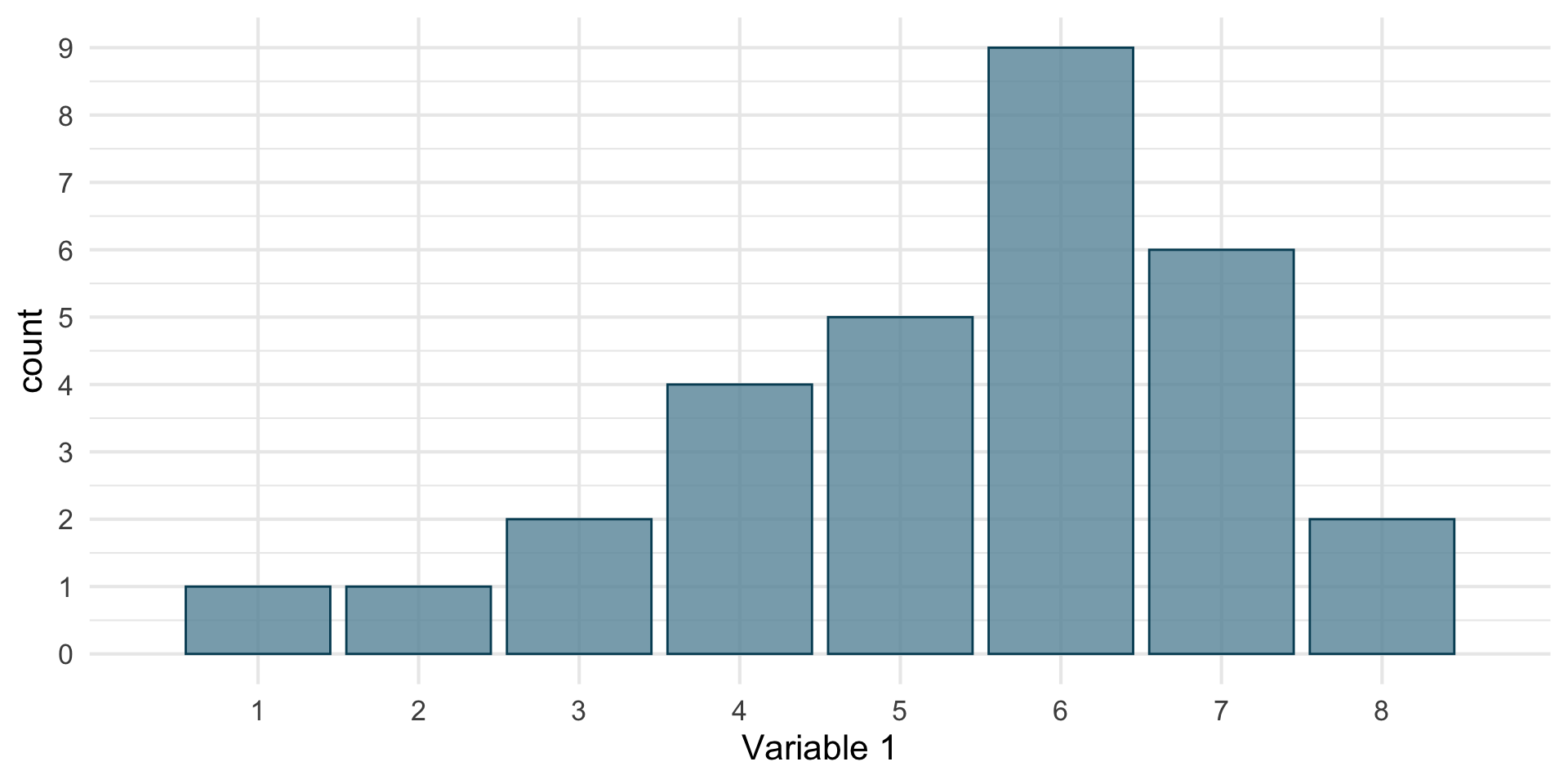
Distributions

Would that also work for this variable?

No! In this case, each value appears only once.

Distributions

This is what the corresponding bar plot would look like

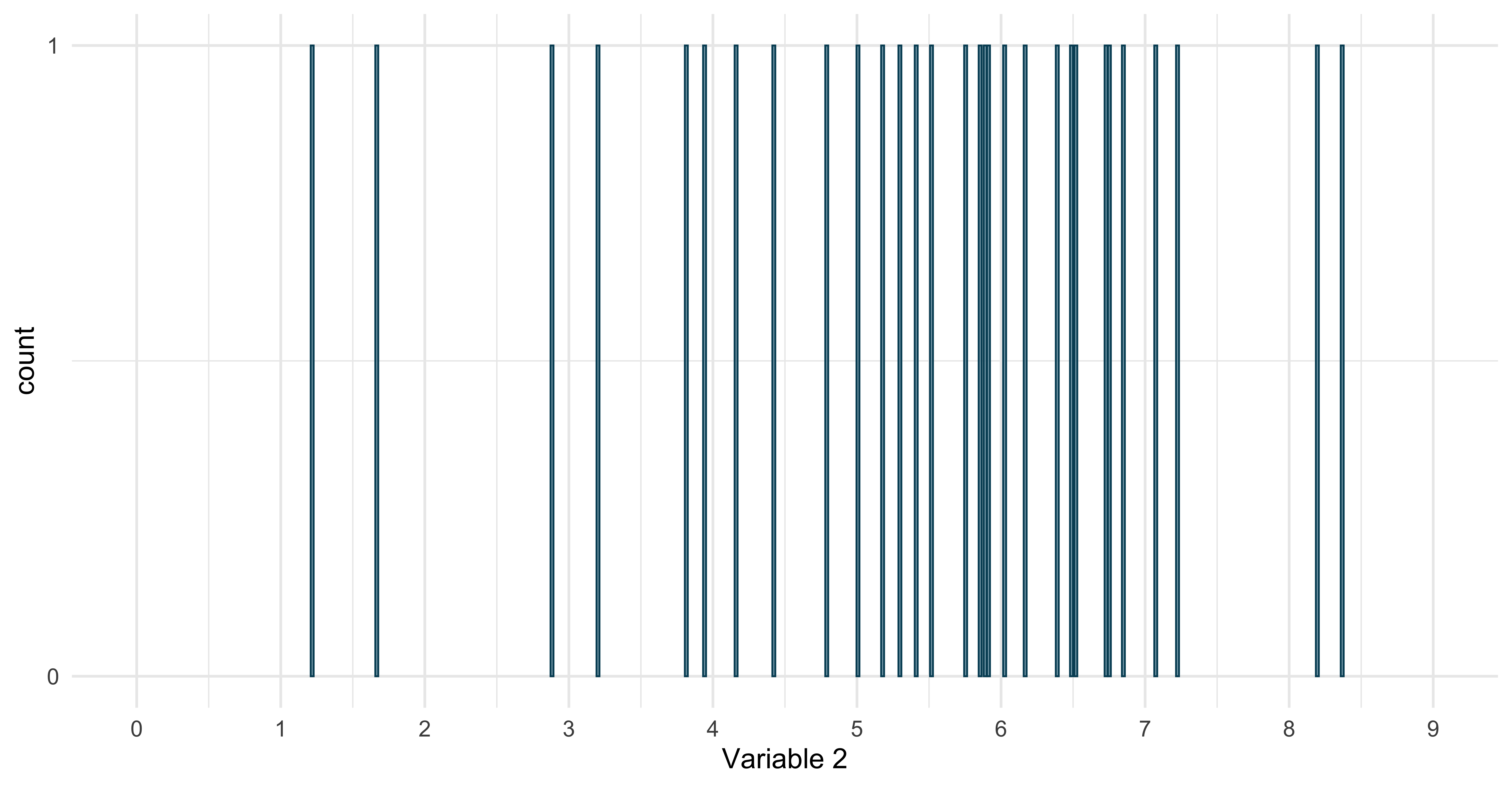
Distributions

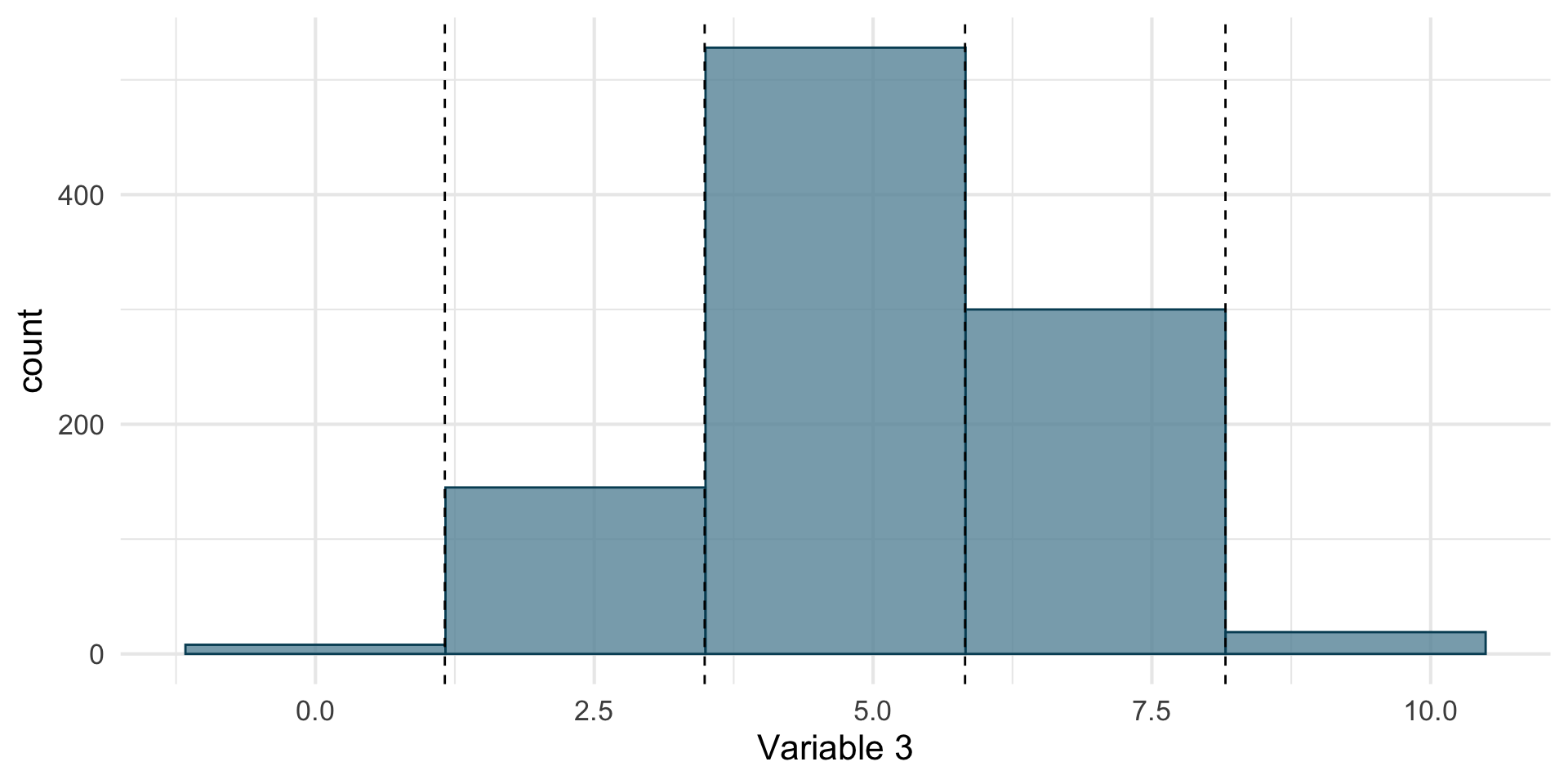
For continuous variables, one solution to get a sense of the distribution is to do a histogram.

Consider for instance the following variable. For clarity each point is shifted vertically by a random amount.

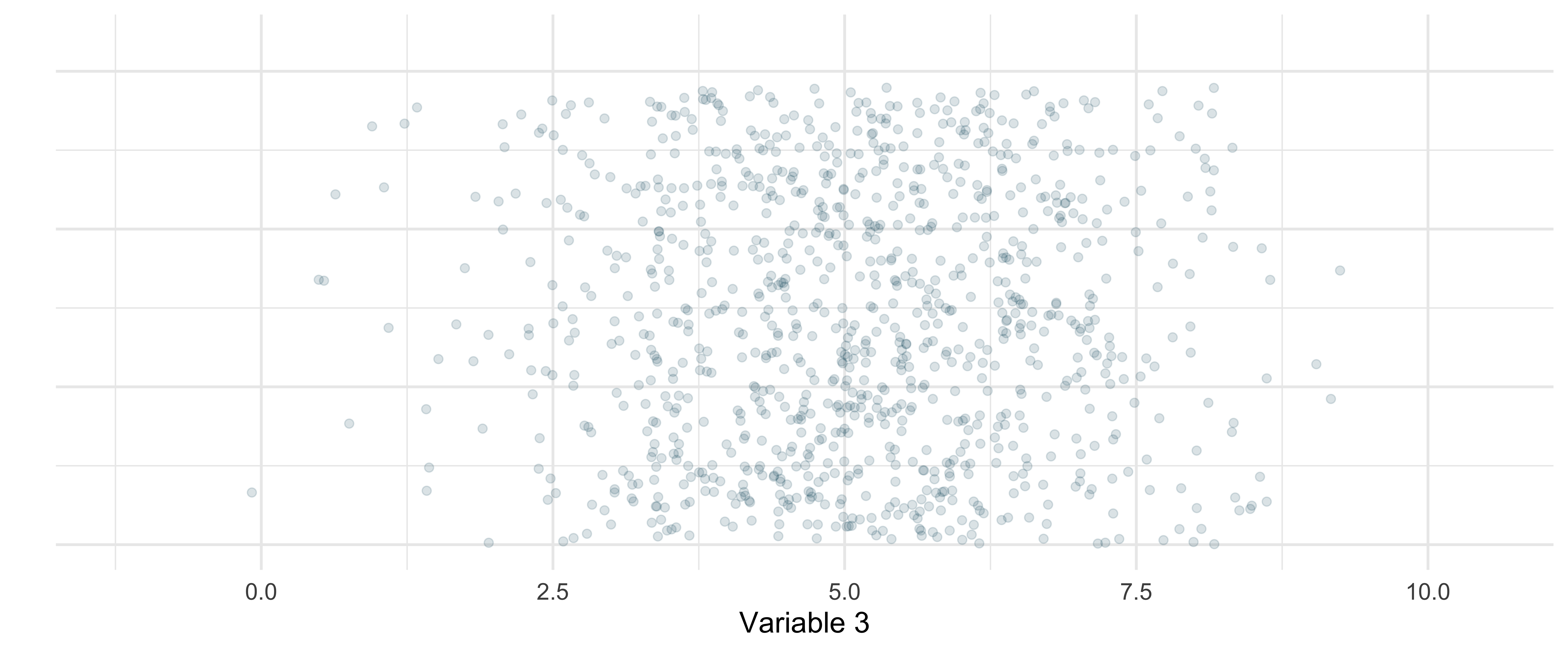
Distributions

We can divide the domain of this variable into 5 bins

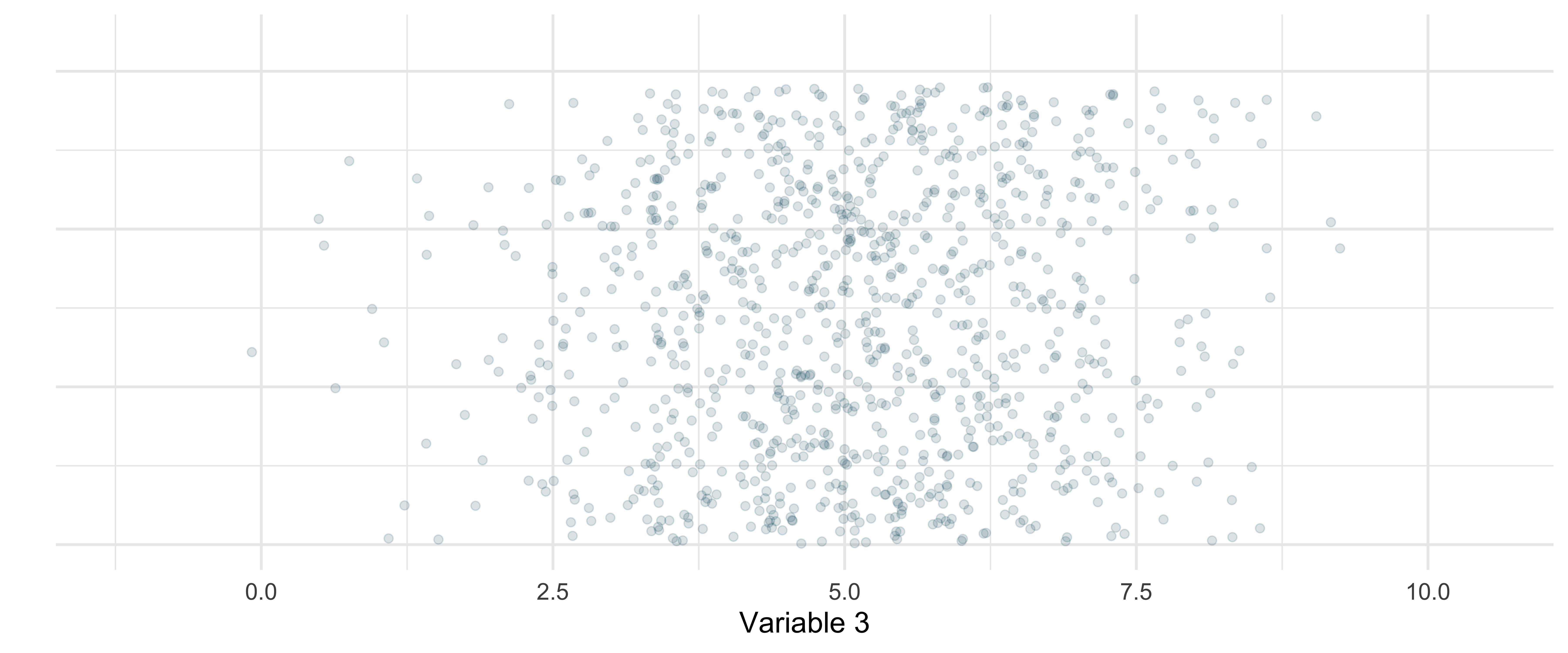
Distributions

We can divide the domain of this variable into 5 bins

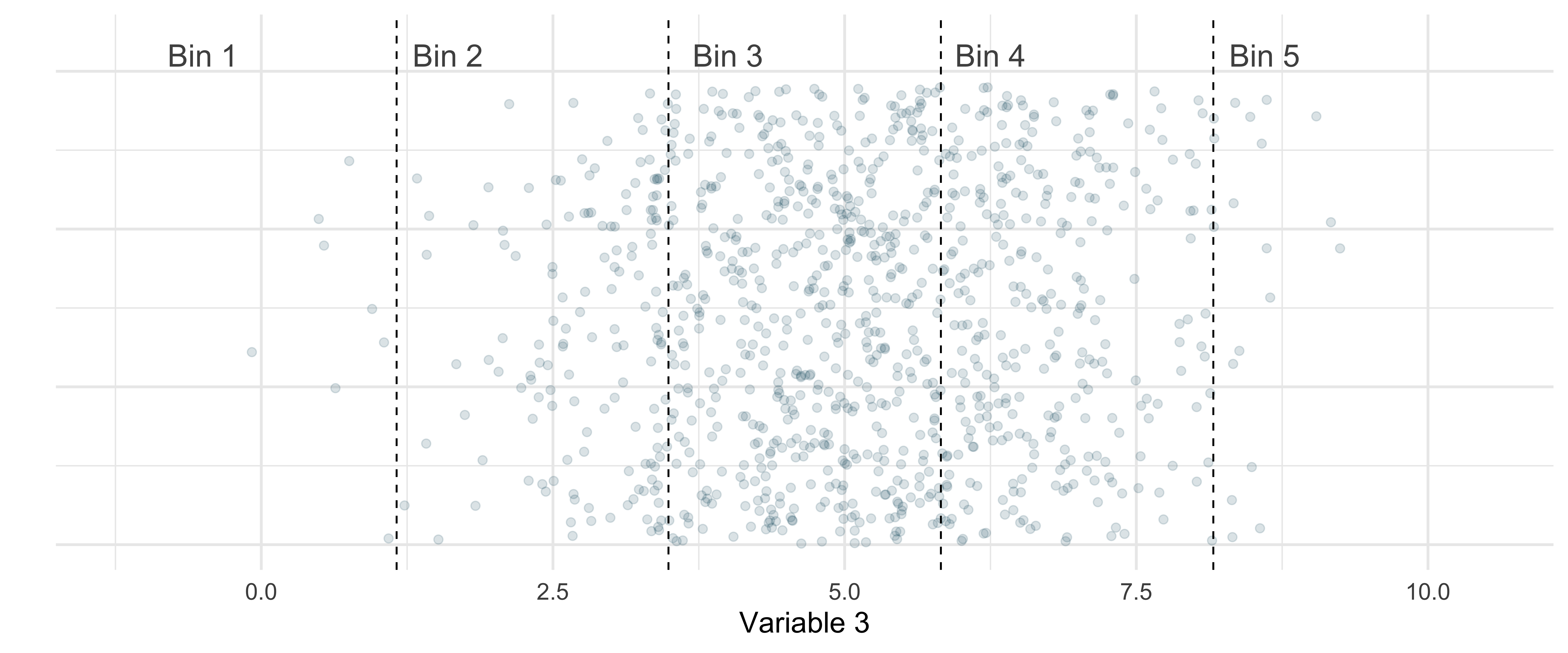
Distributions

And count the number of observations within each bin

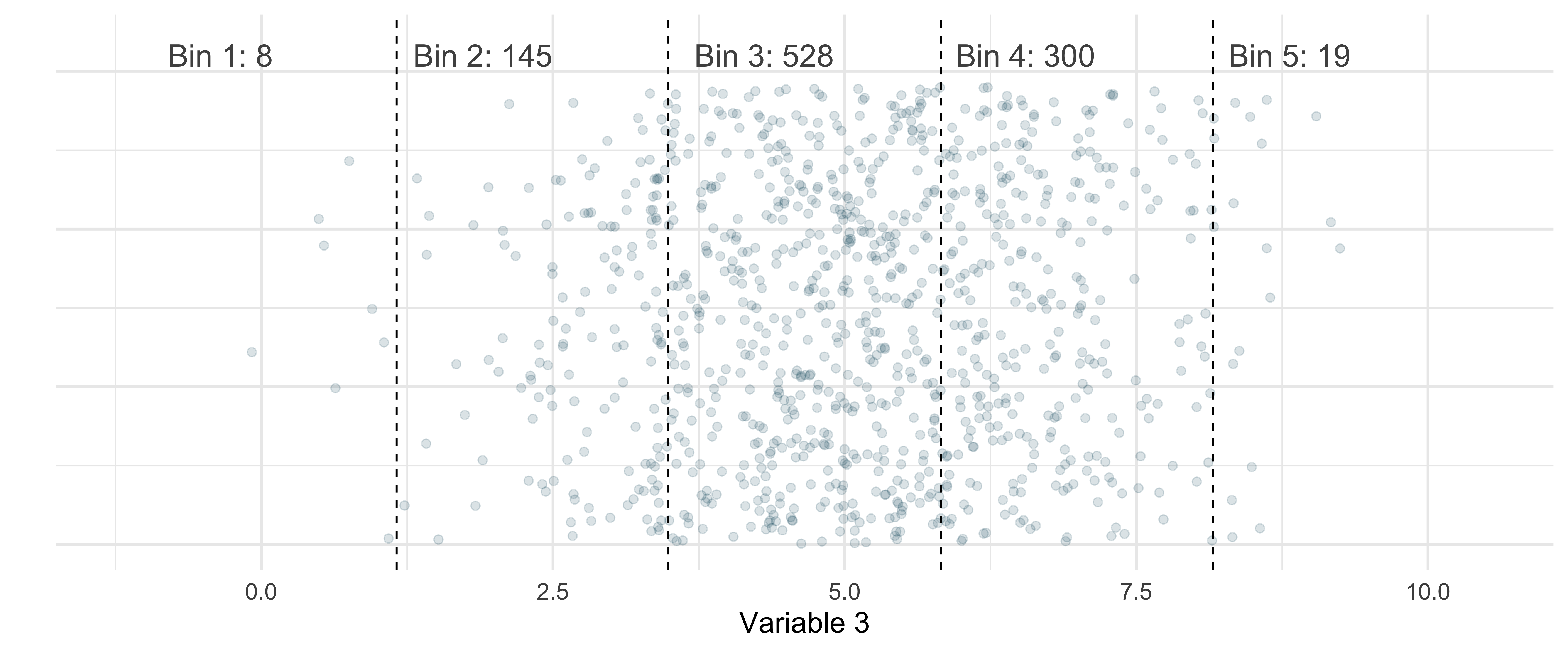
Distributions

If we plot the count per bin, we get a histogram

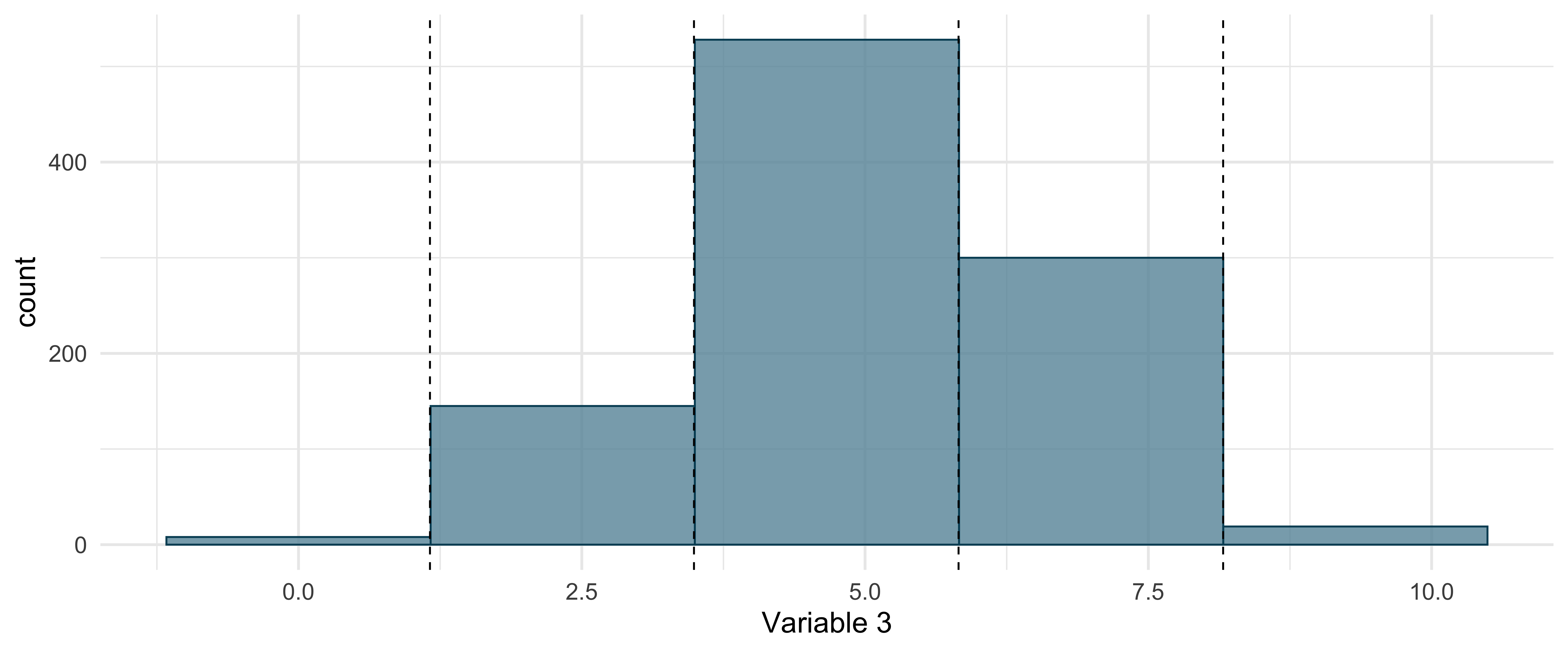
Distributions

There’s no definitive rule to choose the number of bins.

Too few can be misleading, too many can be impractical for visualizing.

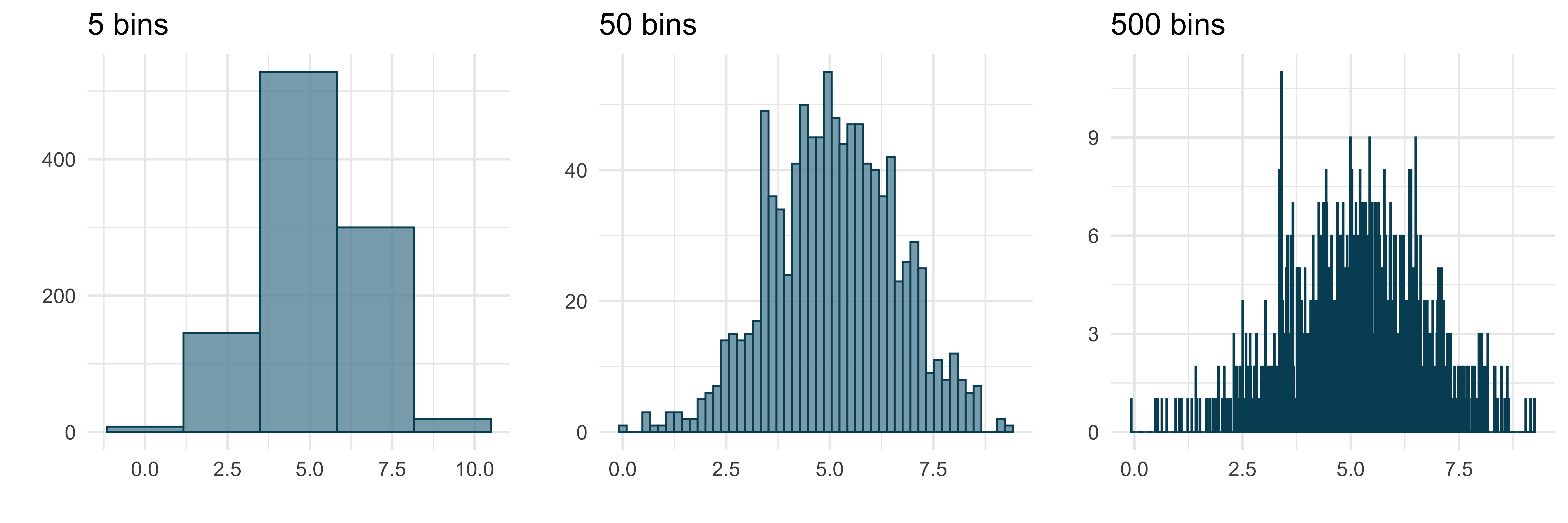
Distributions

Oftentimes, instead of histograms, density plots are used.
- Both are based on the same principle: grouping data points.
- But densities are continuous

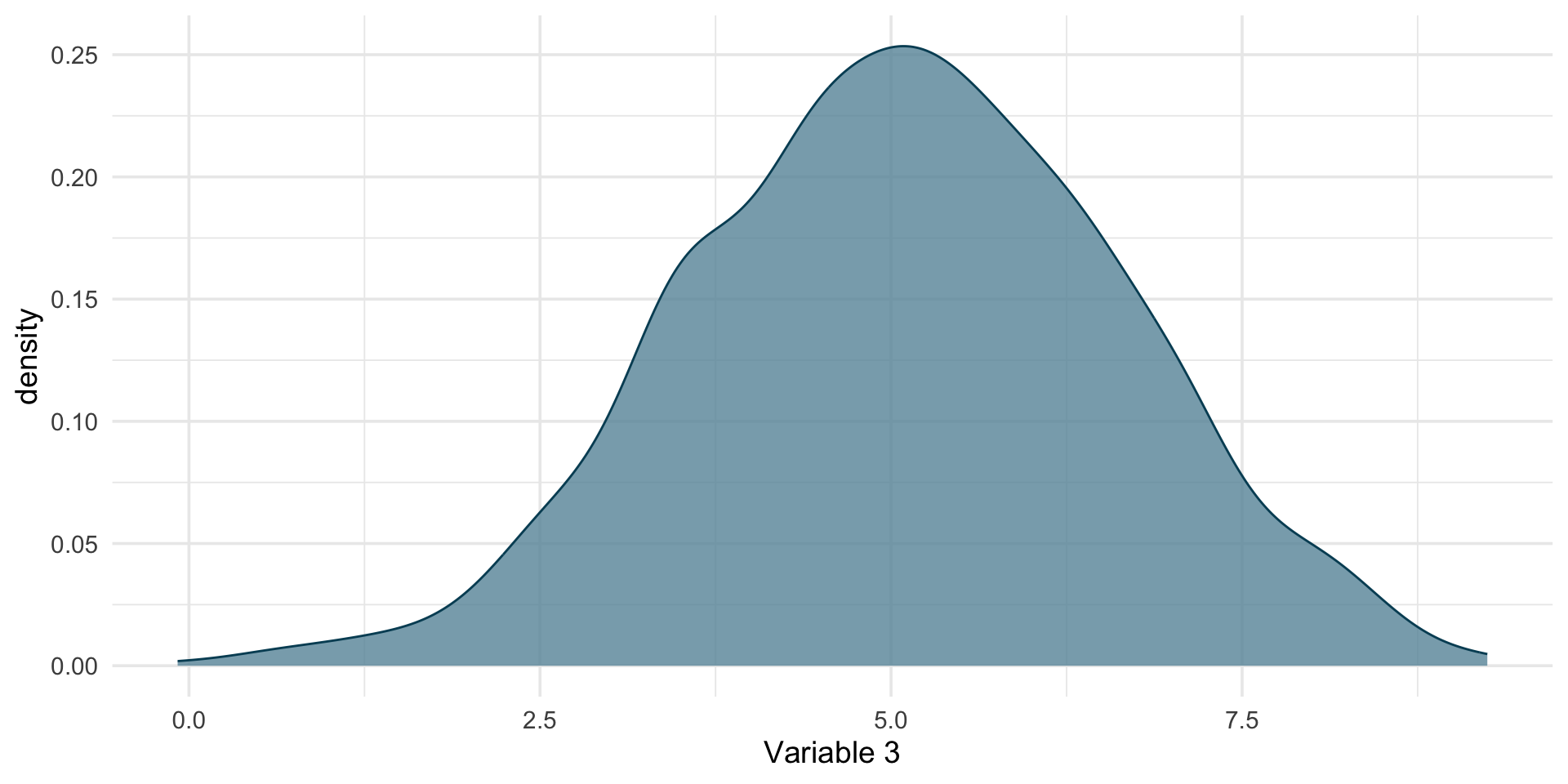
Distributions

You won’t learn how to derive densities in this course
All you need to know: The higher the value on the y-axis, the more observations there are around the corresponding x location
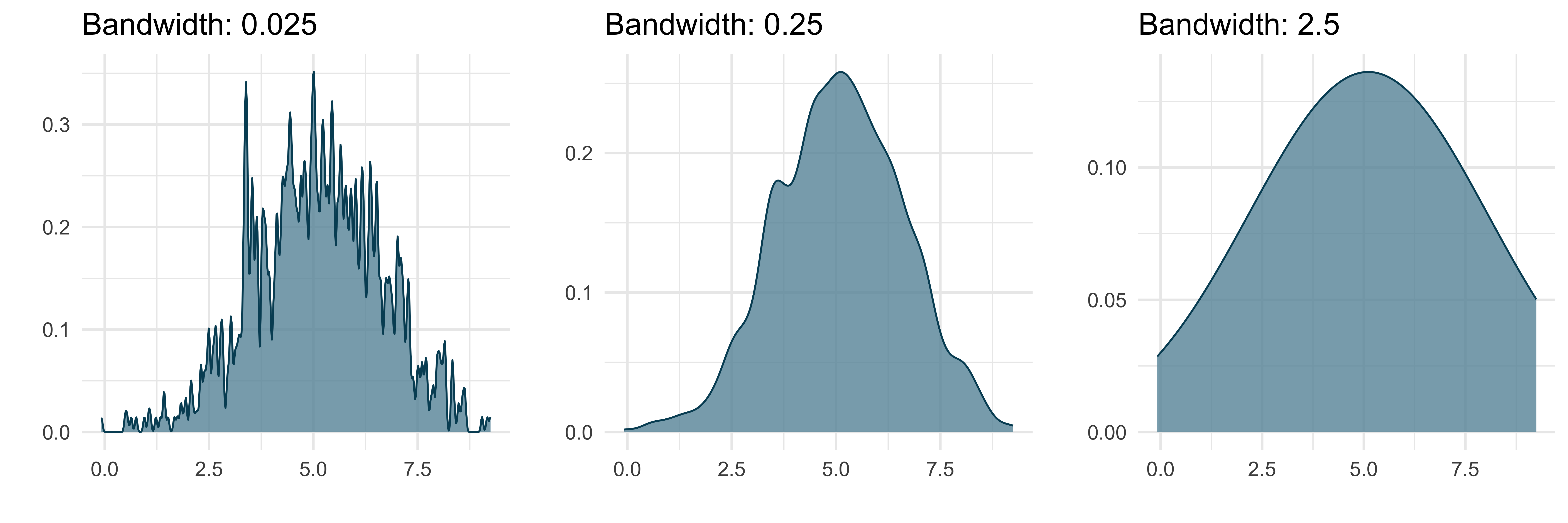
Like the histogram can have a varying number of bins, the density plot can vary in its bandwidth

How to summarize distributions with just a couple of numbers?

(you are probably impatient to hear the answer)

How to summarize distributions with just a couple of numbers?

By describing their central tendency (e.g., mean, median)
And their spread (e.g., standard deviation, inter-quartile range)

Central tendency

Mean

The mean is the most common statistic to describe central tendencies.

The mean is simply the sum of all the grades divided by the number of grades:

\[\bar{x} = \frac{1}{N}\sum_{i = 1}^Nx_i\]

In R, we just need to pass a vector/variable to the mean() function

# make a vector
variable <- c(1, 2, 4, 8, 12)

# calculate the mean
mean(variable)

[1] 5.4

Median

To obtain the median you first need to sort the values.

The median is the value that divides the distribution into two halves

When there is an even number of observations, the median is the average of the last value of the first half and the first value of the second half

\[\text{Med}(x) = \begin{cases} x[\frac{N+1}{2}] & \text{if } N \text{ is odd}\\ \frac{x[\frac{N}{2}]+x[\frac{N}{2}+1]}{2} & \text{if } N \text{ is even} \end{cases}\]

Here, since we have 30 observations, we take the average of the 15th and 16th value:

\[[\frac{6+6}{2}] = 6\]

Median

To obtain the median you first need to sort the values.

In R, we just need to pass a vector/variable to the median() function

# make a vector
variable <- c(1, 2, 4, 8, 12)

# calculate the mean
median(variable)

[1] 4

Mean vs. Median

Which of these two measures of central tendency you use will vary on the context.
Mostly, it will be the mean.

Mean vs. Median

Note, however, that the mean is more sensitive to so called, “outliers”.

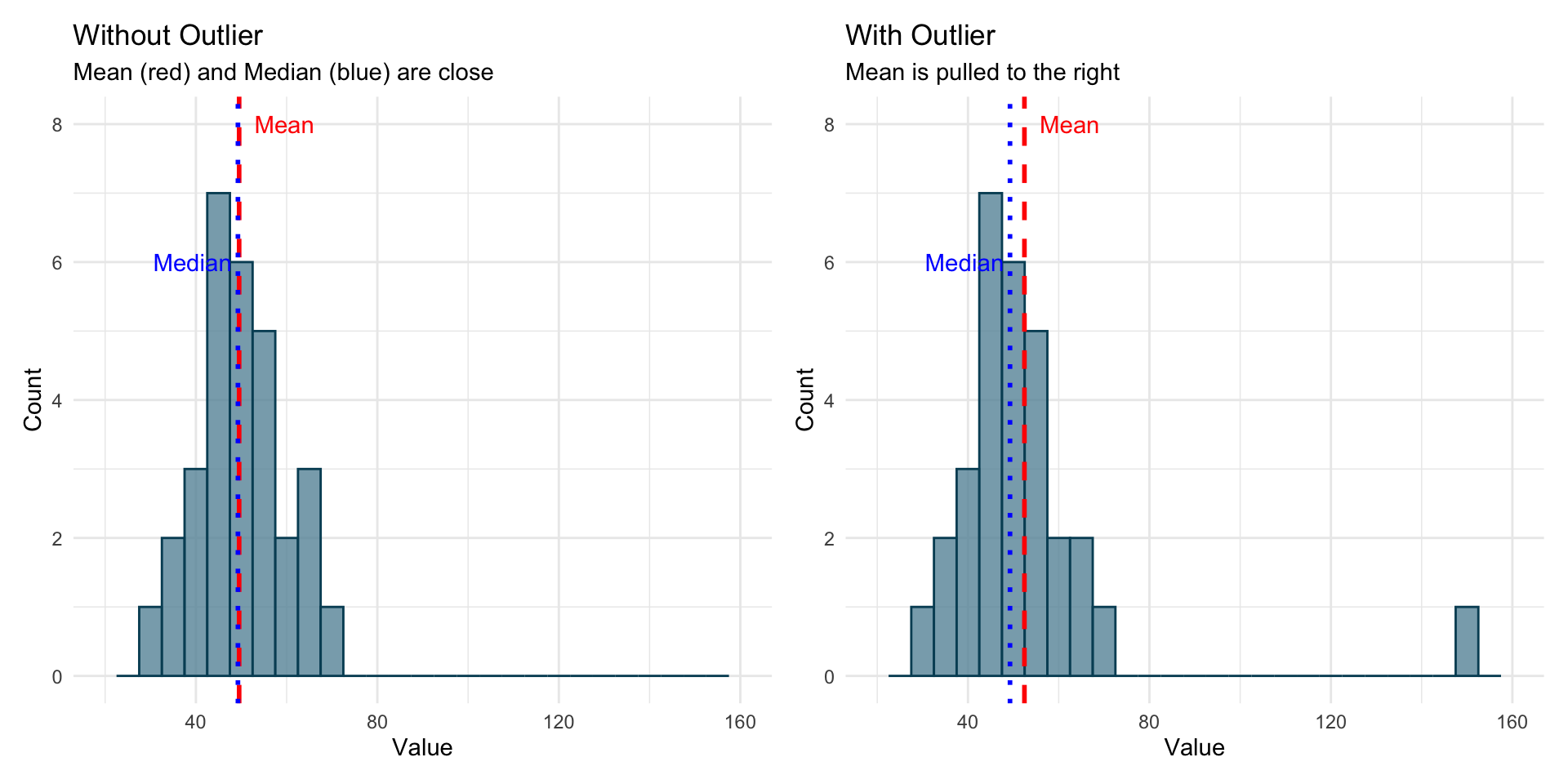
Mean vs. Median in R

Watch out for NAs

Use the na.rm argument and set it to TRUE to remove NAs

[1] NA

[1] 2.5

Spread

We do not only want to now the center of the distribution (mean, median), but also:

How wide is the distribution?

All these have the same mean, but they look quite different.

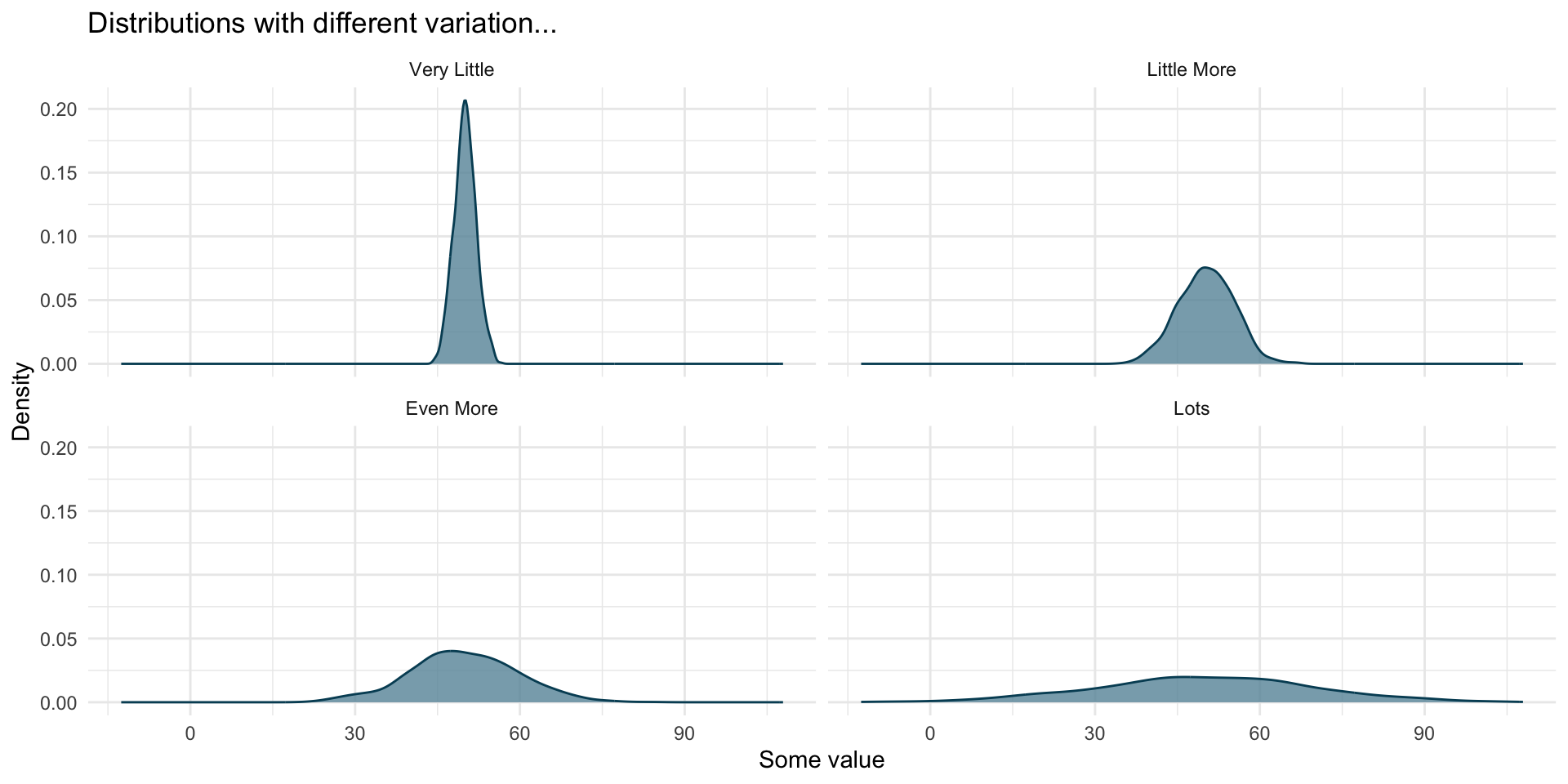
Range, quantiles, and the IQR

One simple way to quantify spread is by calculating the range

distribution <- c(-3, -2, -1, 0, 1, 2, 3)

What would be the range ?

max(distribution) - min(distribution)

[1] 6

However, with outliers, the range is sometimes not ideal.

Range, quantiles, and the IQR

An alternative are quantiles

The median divides the population into 2 groups of equal size
Quartiles divide the population into 4 groups of equal size
There are also terciles, quintiles, deciles, and so on

One way to compute quartiles: divide the ordered variable according to the median

The lower quartile value is the median of the lower half of the data
The upper quartile value is the median of the upper half of the data
If there is an odd number of data points in the original ordered data set, don’t include the median in either half

-3

-2

-1

\[Q_1 = -2,\:\:Q_2 = 0,\:\:Q_3 = 2\]

-3

-2

-1

\[Q_1 = -1.5,\:\:Q_2 = 0,\:\:Q_3 = 1.5\]

Range, quantiles, and the IQR

The interquartile range is the difference between the third and the first quartile:

\(\text{IQR} = Q_3 - Q_1\)

In other words, it corresponds to the bounds of the set which contains the middle half of the distribution

Variance and standard deviation

The variance is a way to quantify how the values of a variable tend to deviate from their mean

If values tend to be close to the mean, then the spread is low
If values tend to be far from the mean, then the spread is large

Can we just take the average deviation from the mean?

x	mean(x)	x - mean(x)
1	2.5	-1.5
4	2.5	1.5
-3	2.5	-5.5
8	2.5	5.5

By construction it would always be 0: values above and under the mean compensate

But we can use the absolute value of each deviation: \(|x_i-\bar{x}|\)
Or their square: \((x_i-\bar{x})^2\)

Variance and standard deviation

This is how the variance is computed: by averaging the squared deviations from the mean

\[\text{Var}(x) = \frac{1}{N}\sum_{i = 1}^N(x_i-\bar{x})^2\]

Because the variance is a sum of squares, it can get quite big compared to the other statistics like the mean, the median or the interquartile range.
To express the spread in the same unit as the data, we can take the square root of the variance, which is called the standard deviation

\[\text{SD}(x) = \sqrt{\text{Var}(x)} = \sqrt{\frac{1}{N}\sum_{i = 1}^N(x_i-\bar{x})^2}\]

Computing spread in R

Interquartile range (IQR)

variable <- c(0, 1, 3, 4, 6, 7, 8, 10, 11)
IQR(variable)

[1] 5

Standard deviation (sd)

sd(variable)

[1] 3.844188

You can obtain the quantiles of a variable using the quantile() function (the default are quartiles)

quantile(variable)

  0%  25%  50%  75% 100% 
   0    3    6    8   11

Variables, Distributions and Summary Statistics

Today we learn how to describe data

Variables

Variables

Variables

Variables

Variables

Variables

Variables

Variables

Variables

Variables

Variables

Overview Variable Types

Distributions

Distributions

Distributions

Distributions

Distributions

Distributions

Distributions

Distributions

Distributions

Distributions

Distributions

Distributions

Distributions

Distributions

Central tendency

Mean

Median

Median

Mean vs. Median

Mean vs. Median

Mean vs. Median in R

Spread

Range, quantiles, and the IQR

Range, quantiles, and the IQR

Range, quantiles, and the IQR

Variance and standard deviation

Variance and standard deviation

Computing spread in R

That’s it for today :)