Linear Regression

Overview

1. Drawing Lines

2. Running a regression in R

3. Statistical Inference for Regression

Drawing Lines

Essential parts of regression

Y

“Outcome”/“Dependent”/“Response” variable

Thing you want to explain or predict

X

“Explanatory”/“Independent”/“Predictor” variable

Thing you use to explain or predict Y

For example, Does eating cookies make people happier?

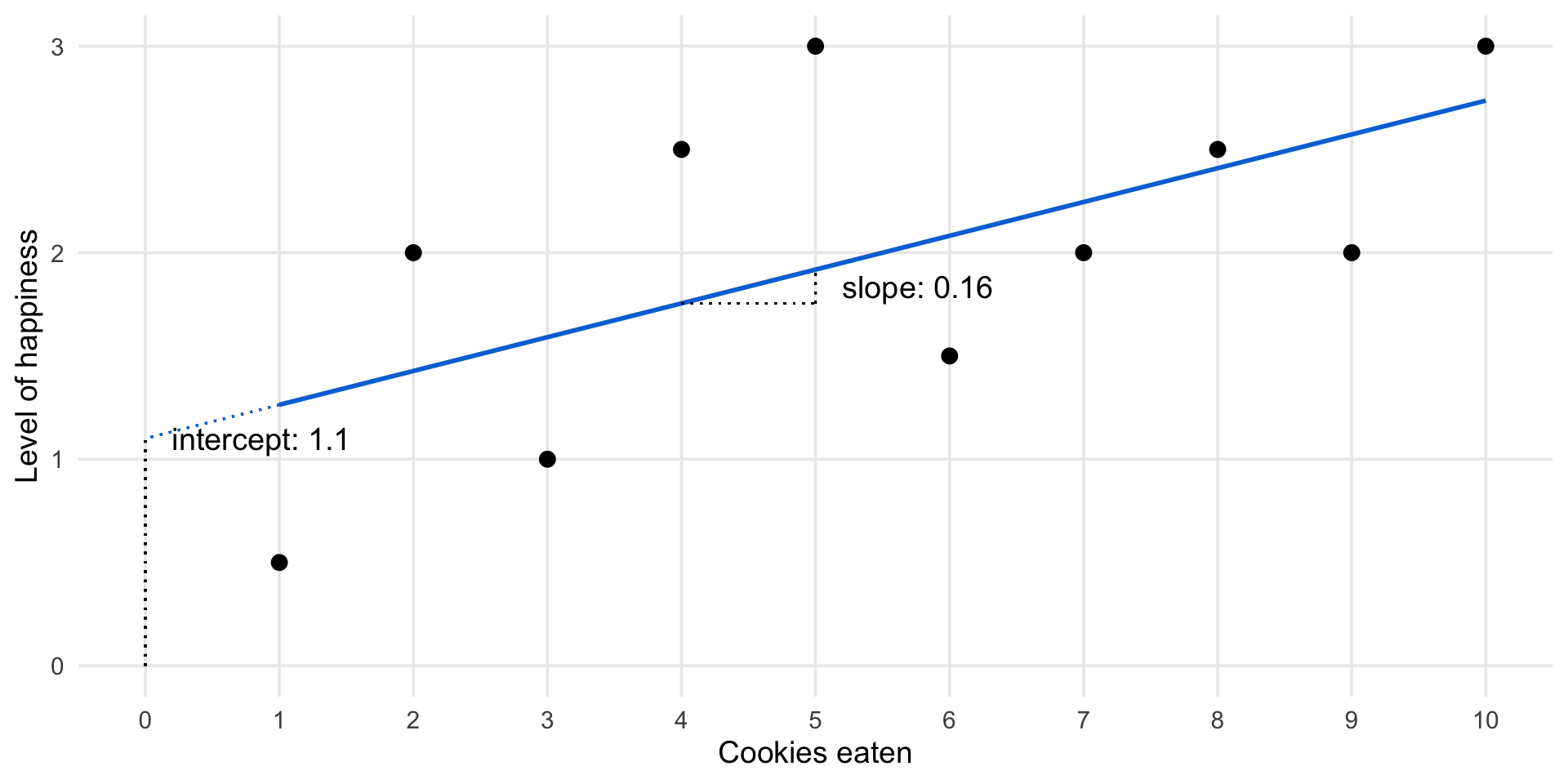
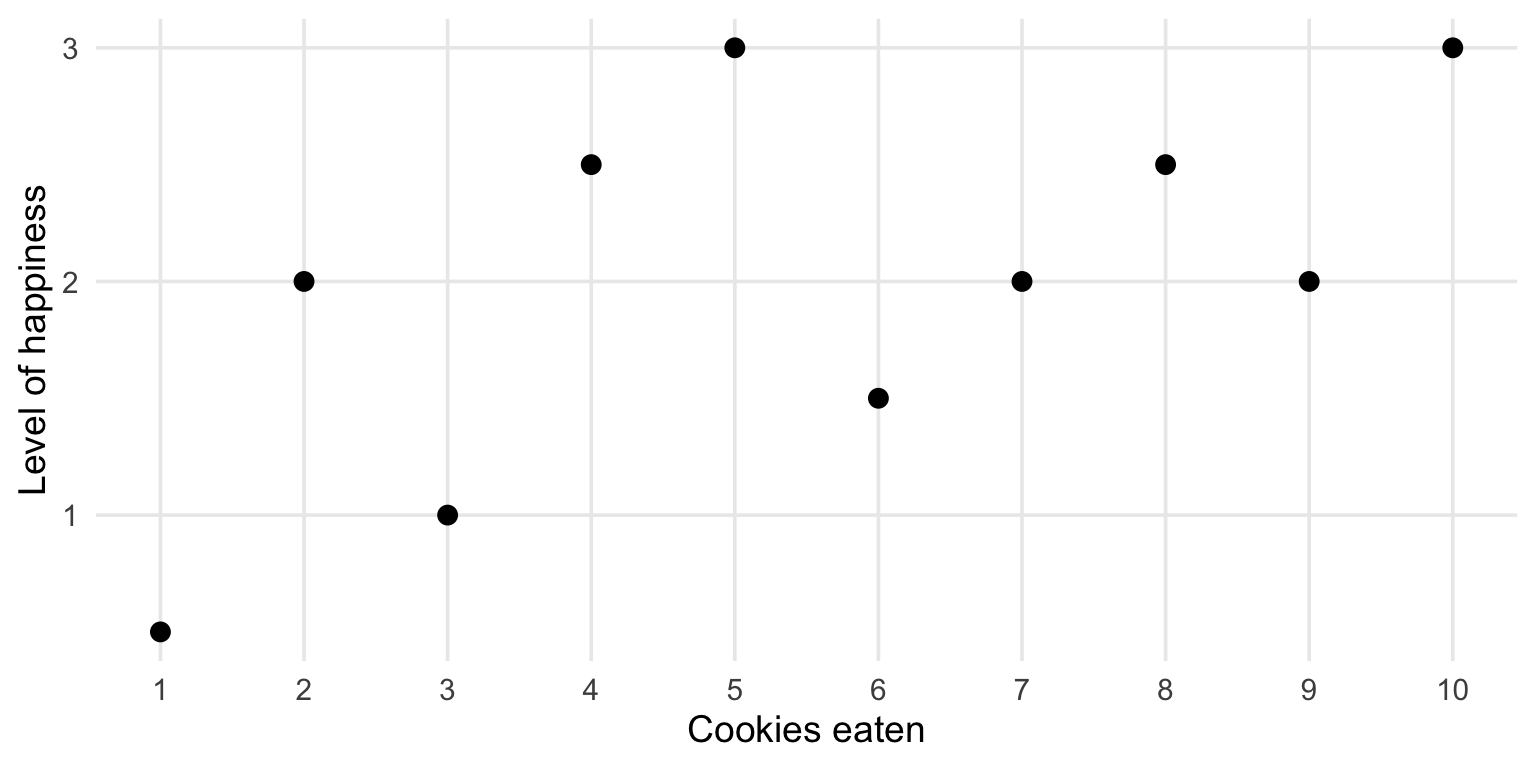
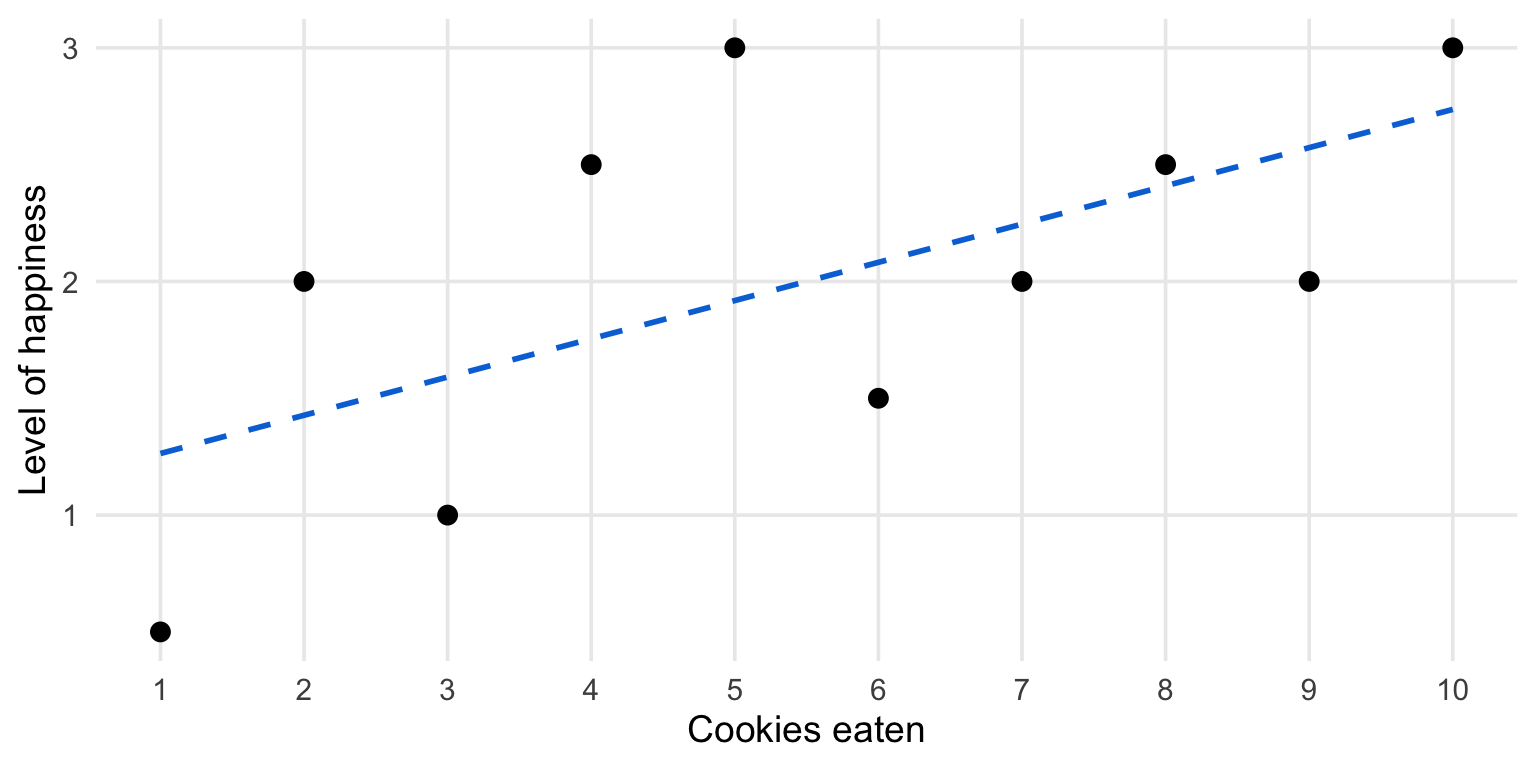
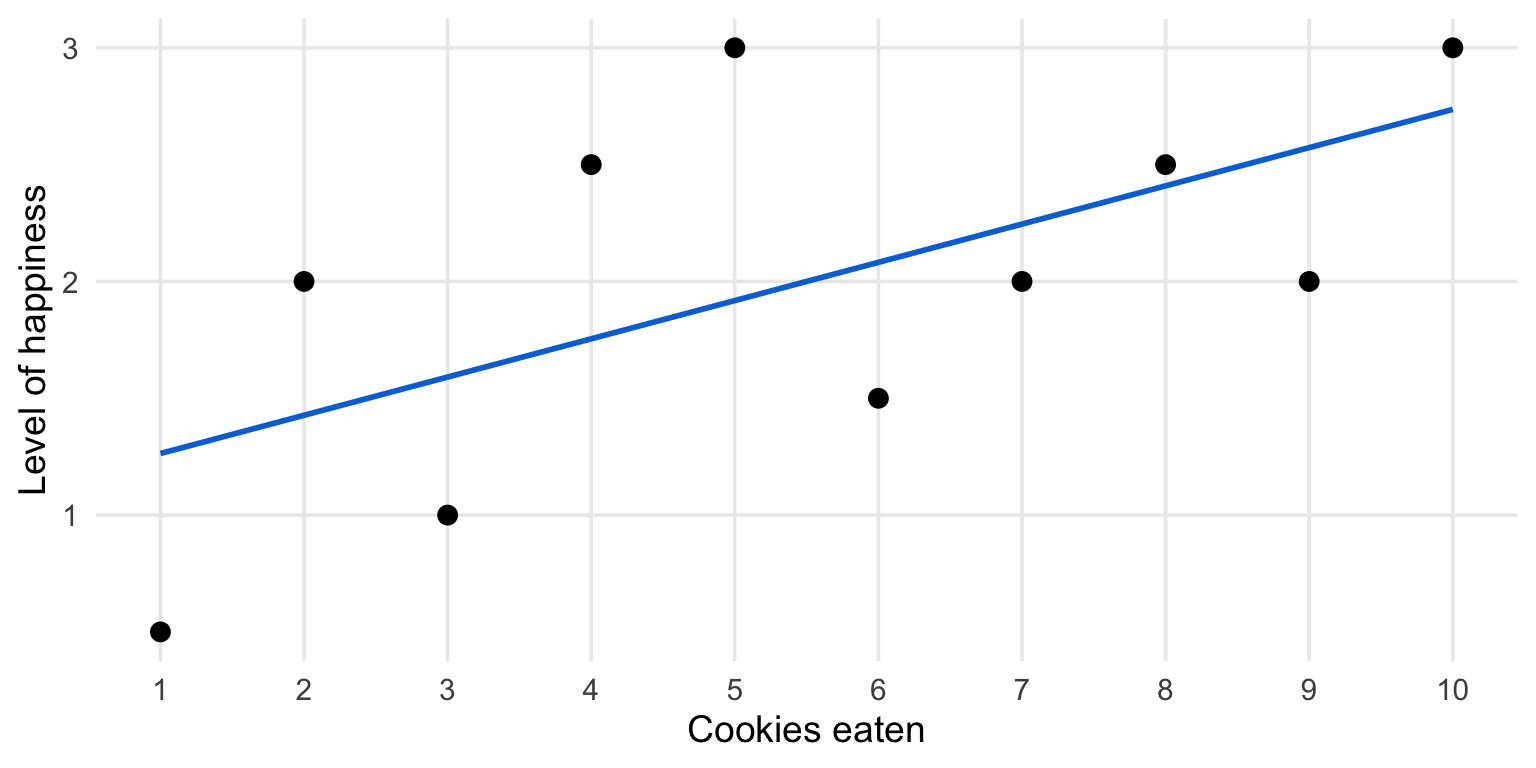
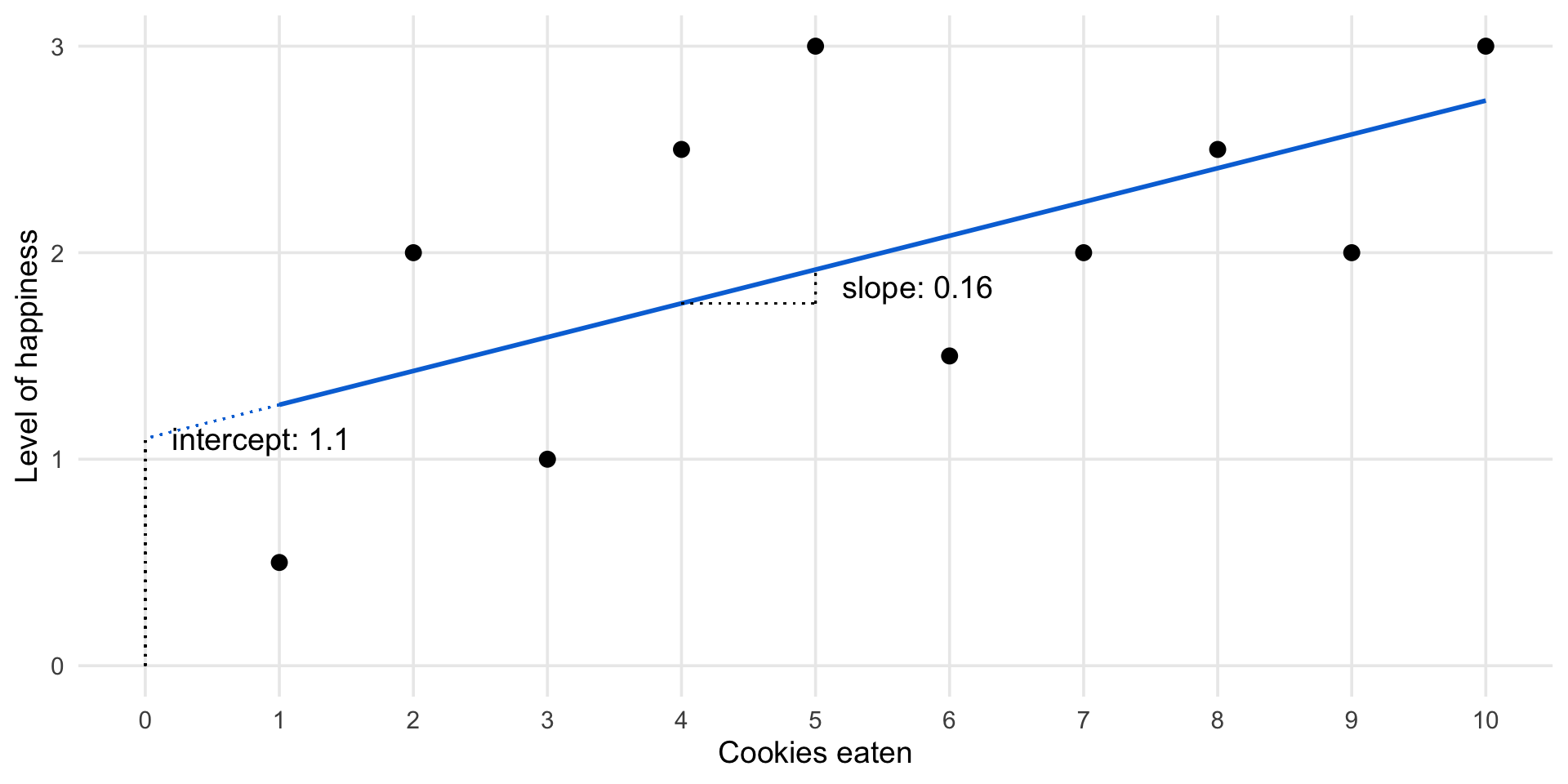
Cookies and happiness

How to do regression?

1. Plot X and Y

2. Draw a line that approximates the relationship

3. Find out the slope and intercept of the line

How good is the fit?

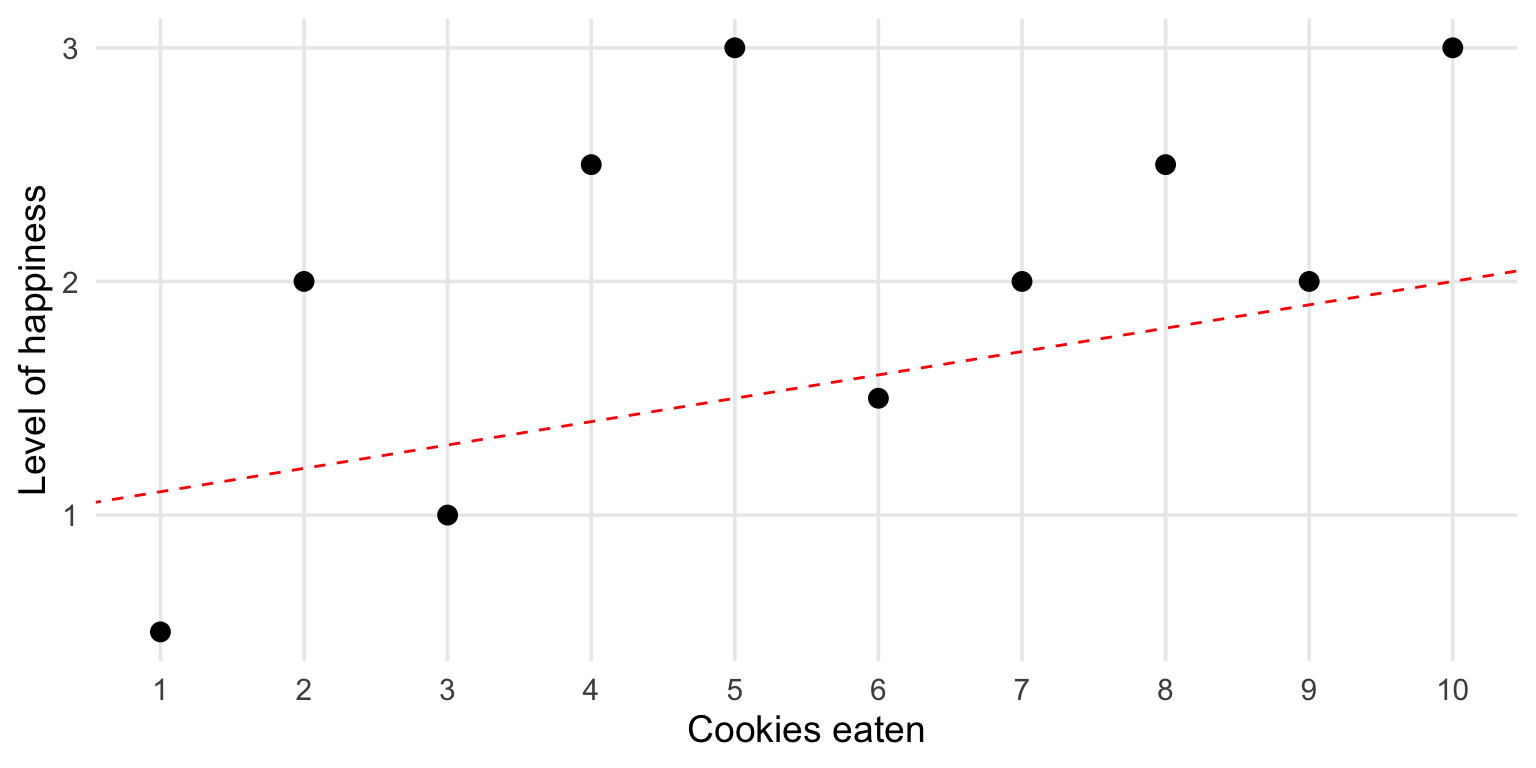
How good is the fit?

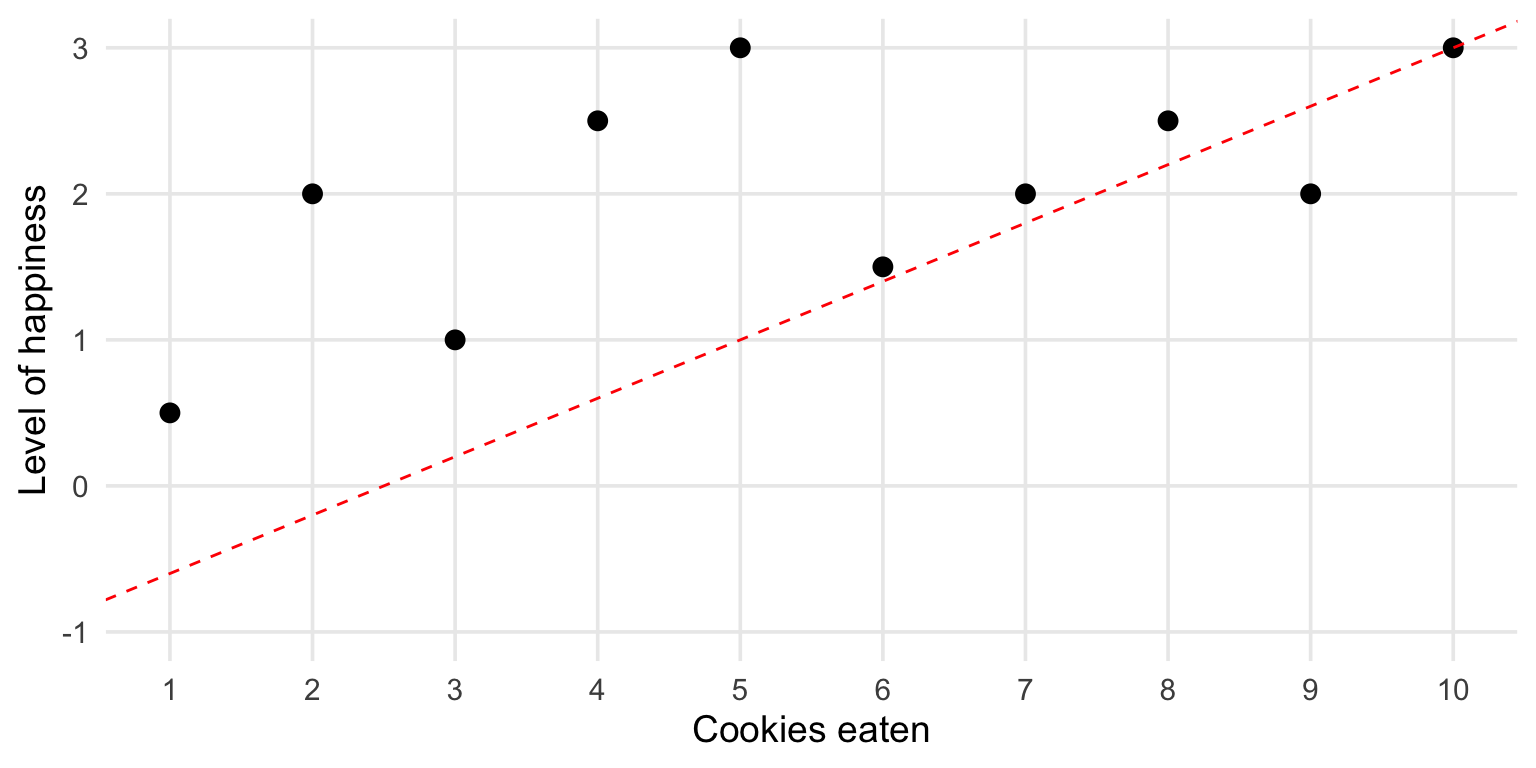
How good is the fit?

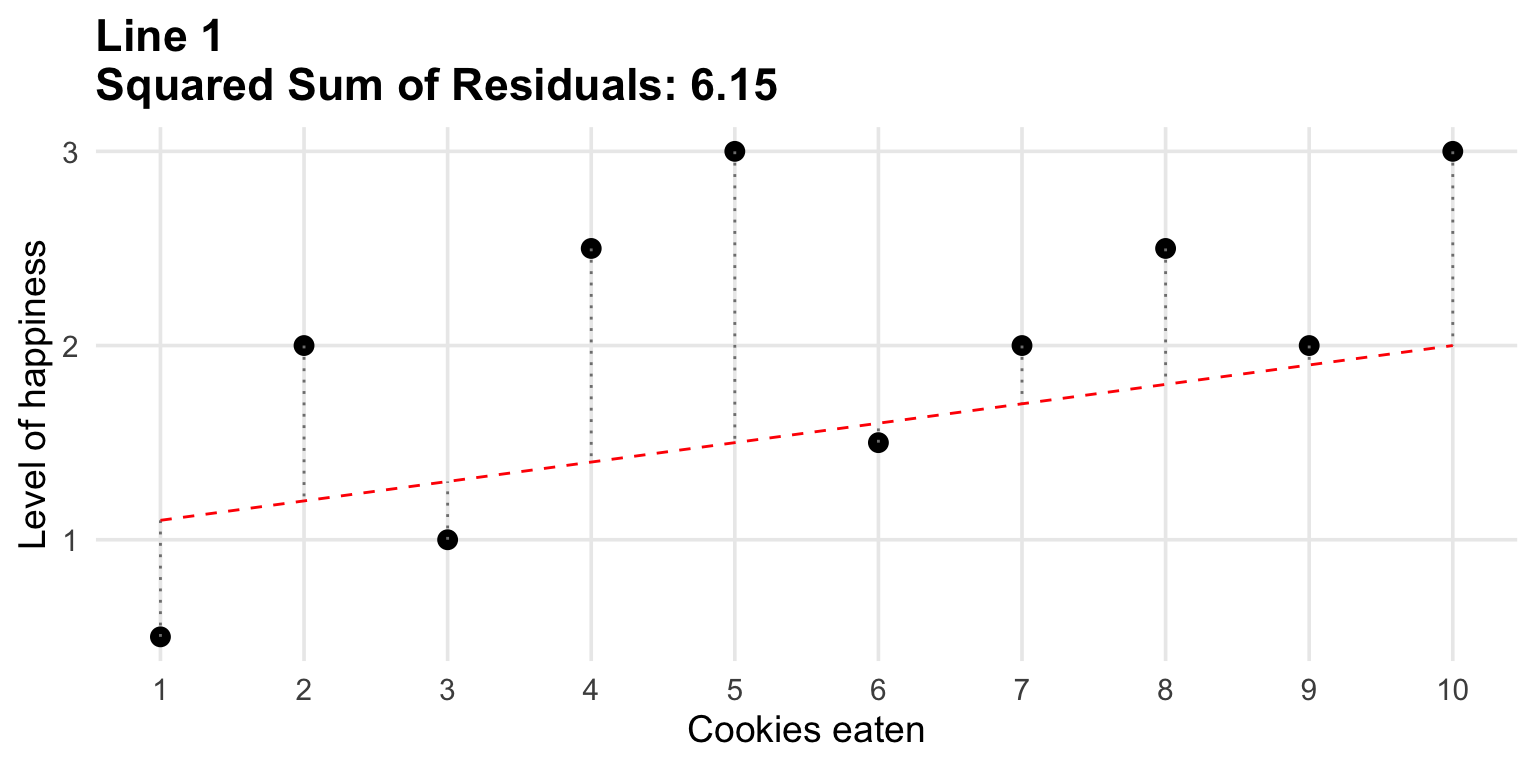
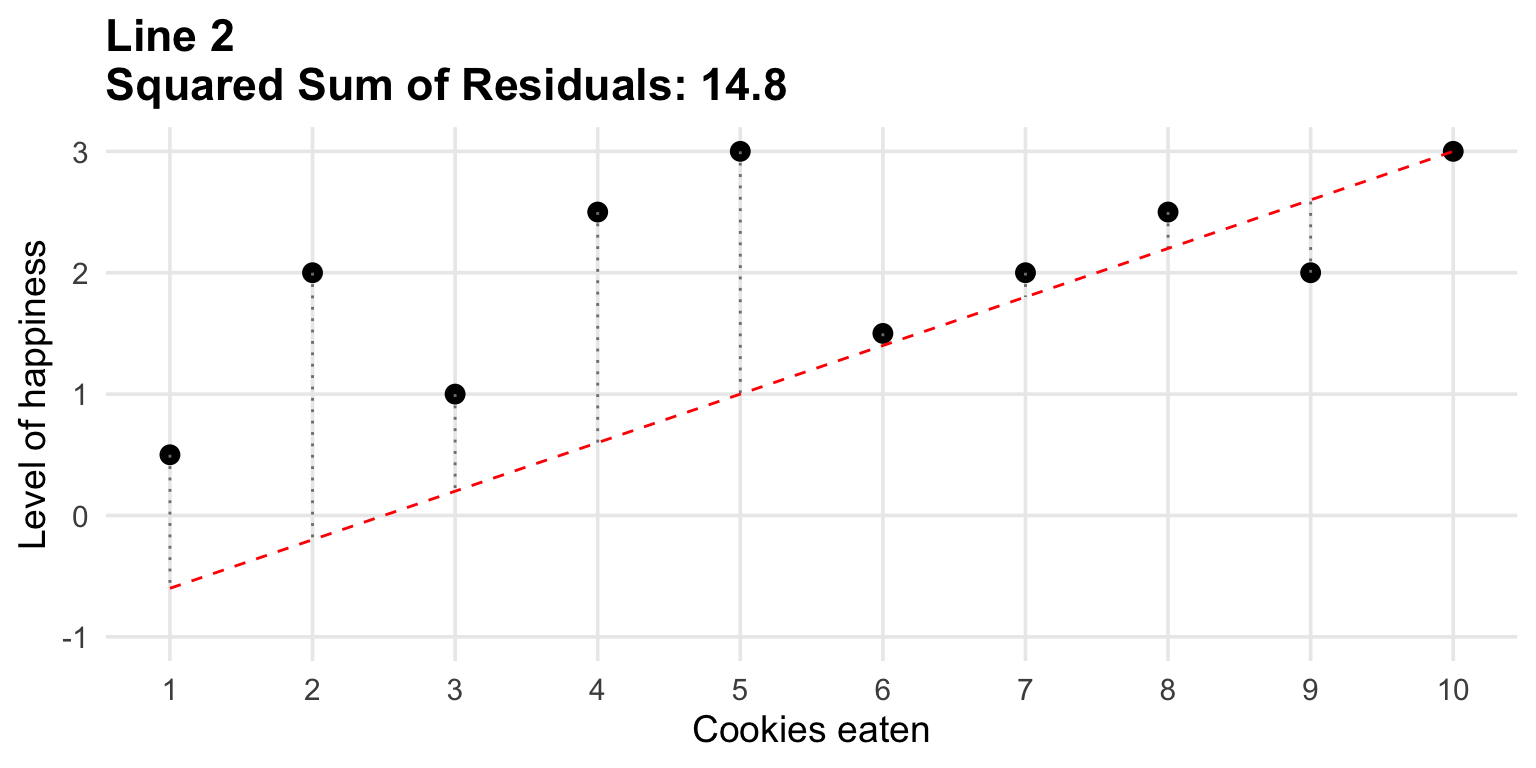
Residuals

We don’t need to rely on our visual intuition. We can calculate how well the line fits our data.

Residual = difference between the observed and predicted values of the dependent variable

(i.e. distance of a data point to the line, for a given value of X)

For example, if someone who ate 5 cookies reported a happiness level of 2.5, but the regression predicts 2.0, the residual is:

\(2.5−2.0=0.5\)

Ordinary Least Squares (OLS)

Goal of regression: minimize residuals

A (not so good solution): Take the sum of all residuals

• some residuals are negative, some are positive, they will cancel out

A better solution: Square all residuals, then sum them

• this is a strategy we’ve already seen for calculating standard deviations.

Why not just use absolute values?

It is mathematically a lot easier to find the minimum of squared sums.

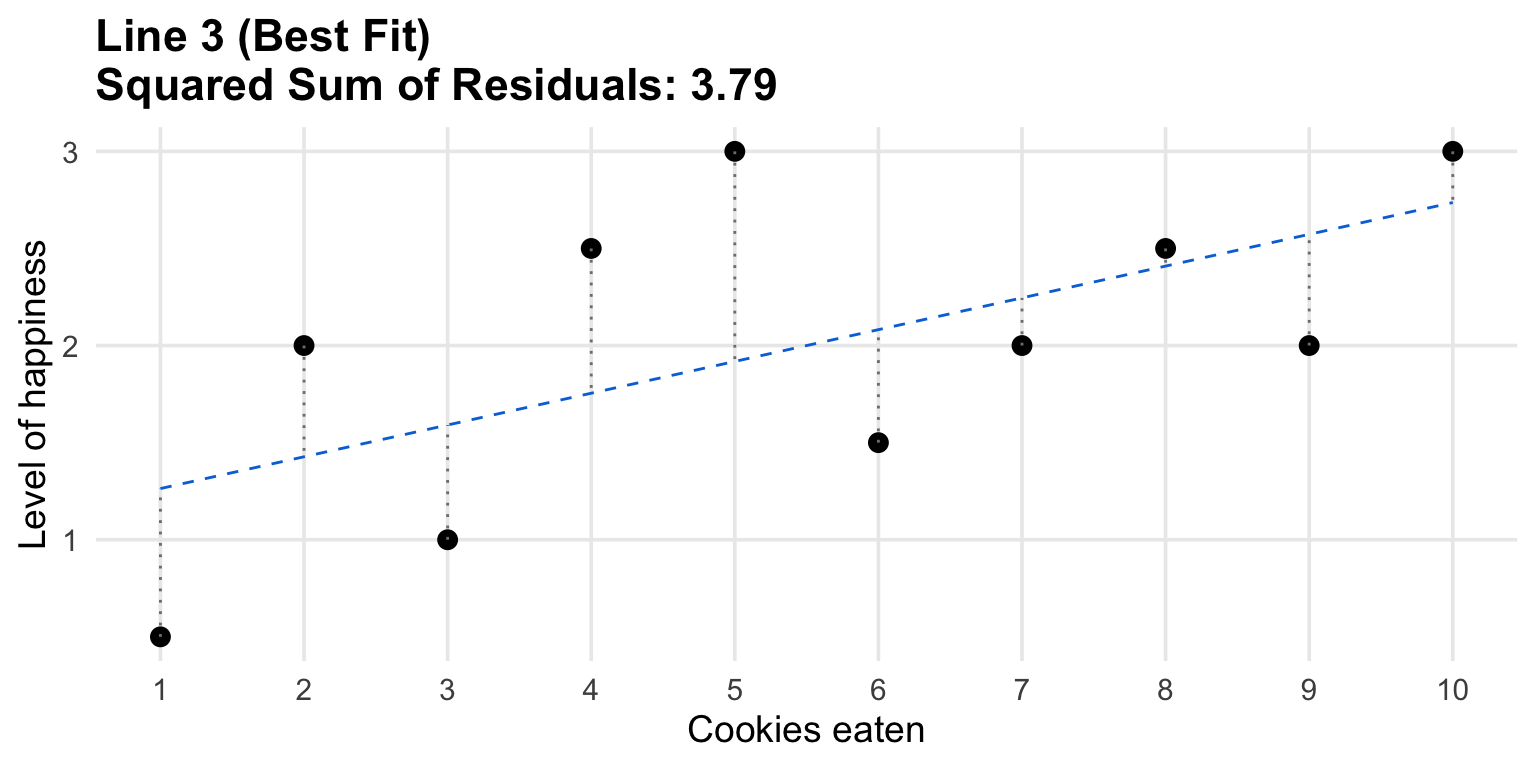
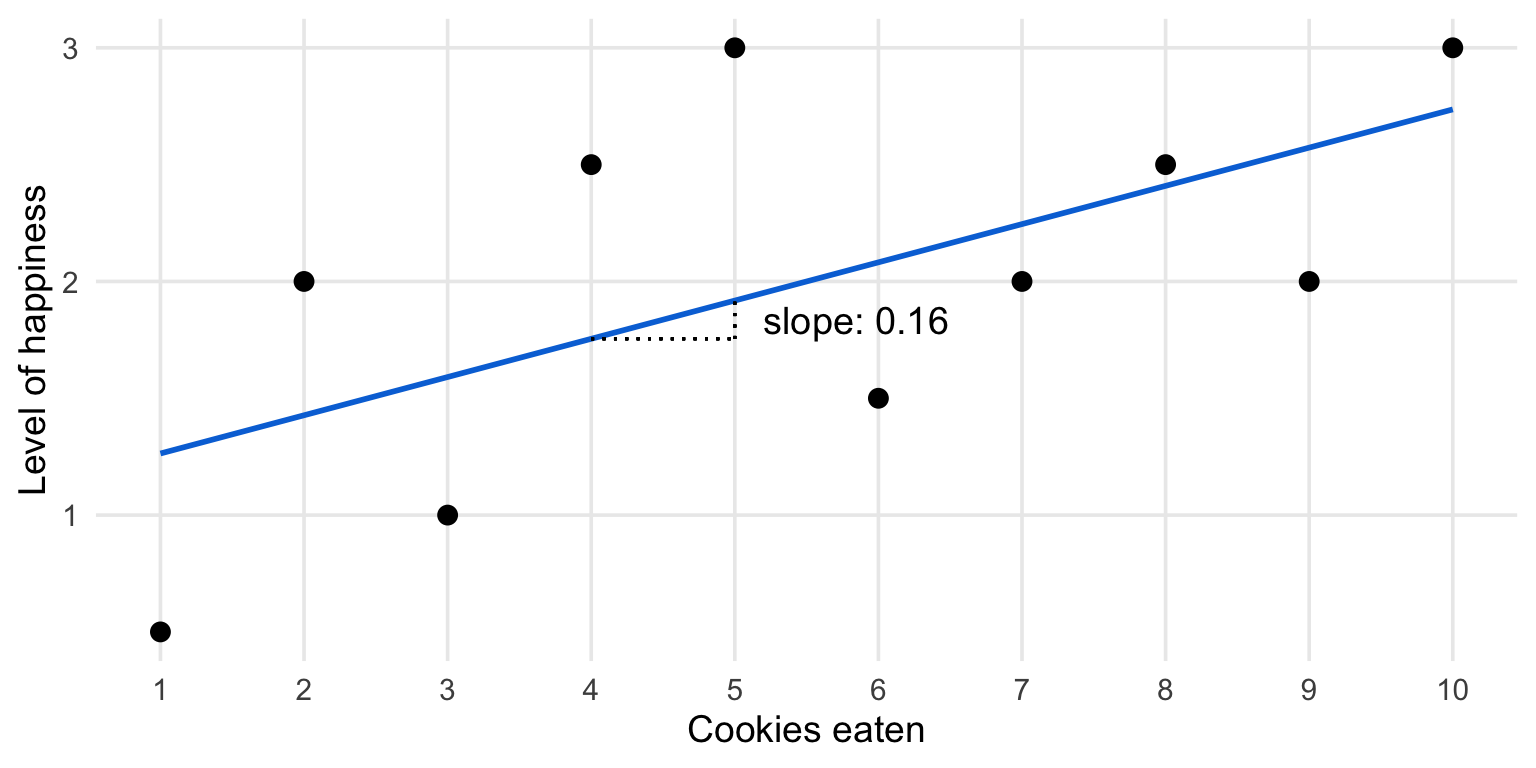
Linear regression estimates

Linear regression estimates

Linear regression estimates

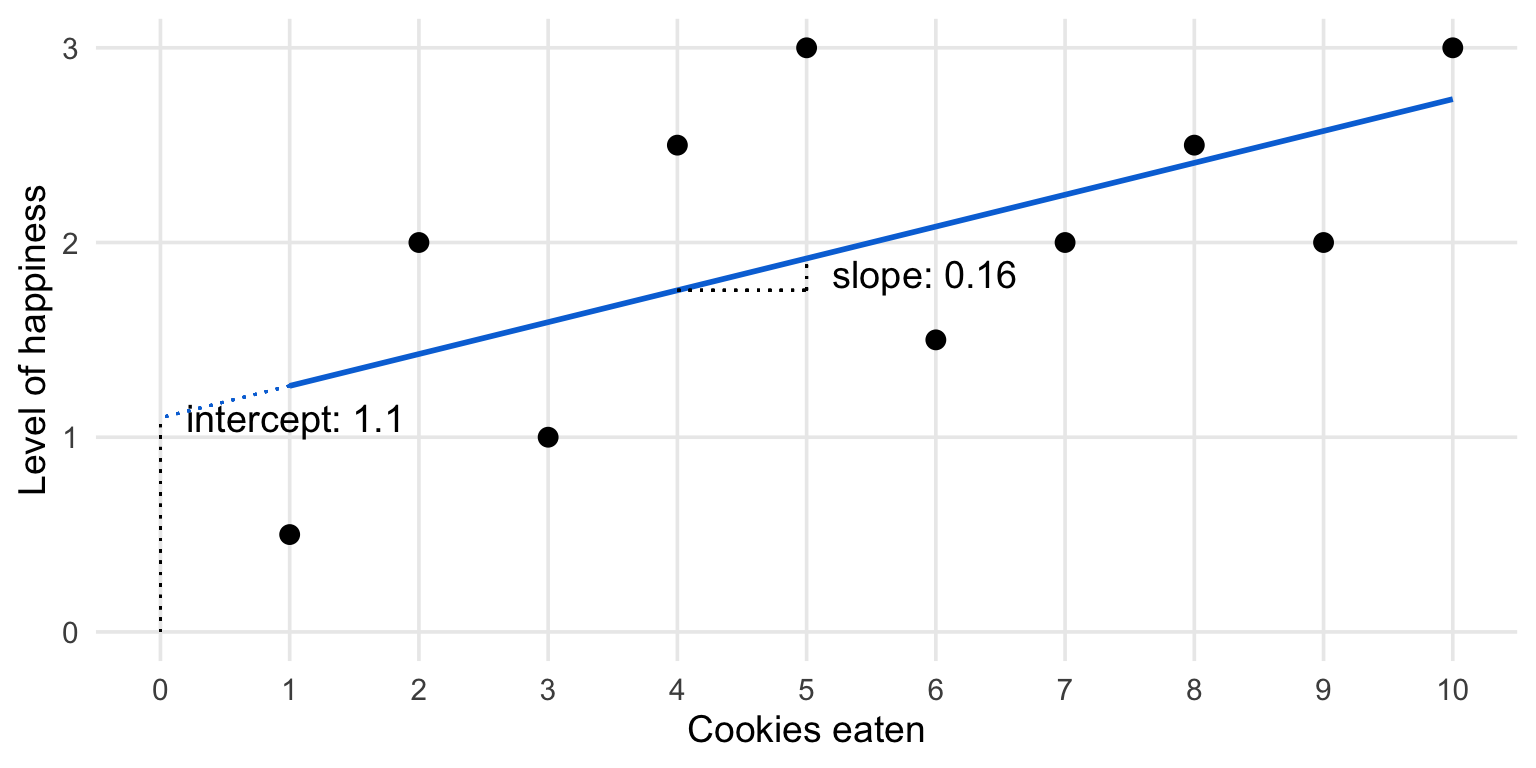
Interpreting linear regression output

“A one unit increase in X is associated with a beta 1 increase (or decrease) in Y, on average.”

# Compute the OLS regression model
lm(happiness ~ cookies, data = cookies)

Call:
lm(formula = happiness ~ cookies, data = cookies)

Coefficients:
(Intercept)      cookies  
     1.1000       0.1636  

Interpreting linear regression output

“A one unit increase in X is associated with a beta 1 increase (or decrease) in Y, on average.”

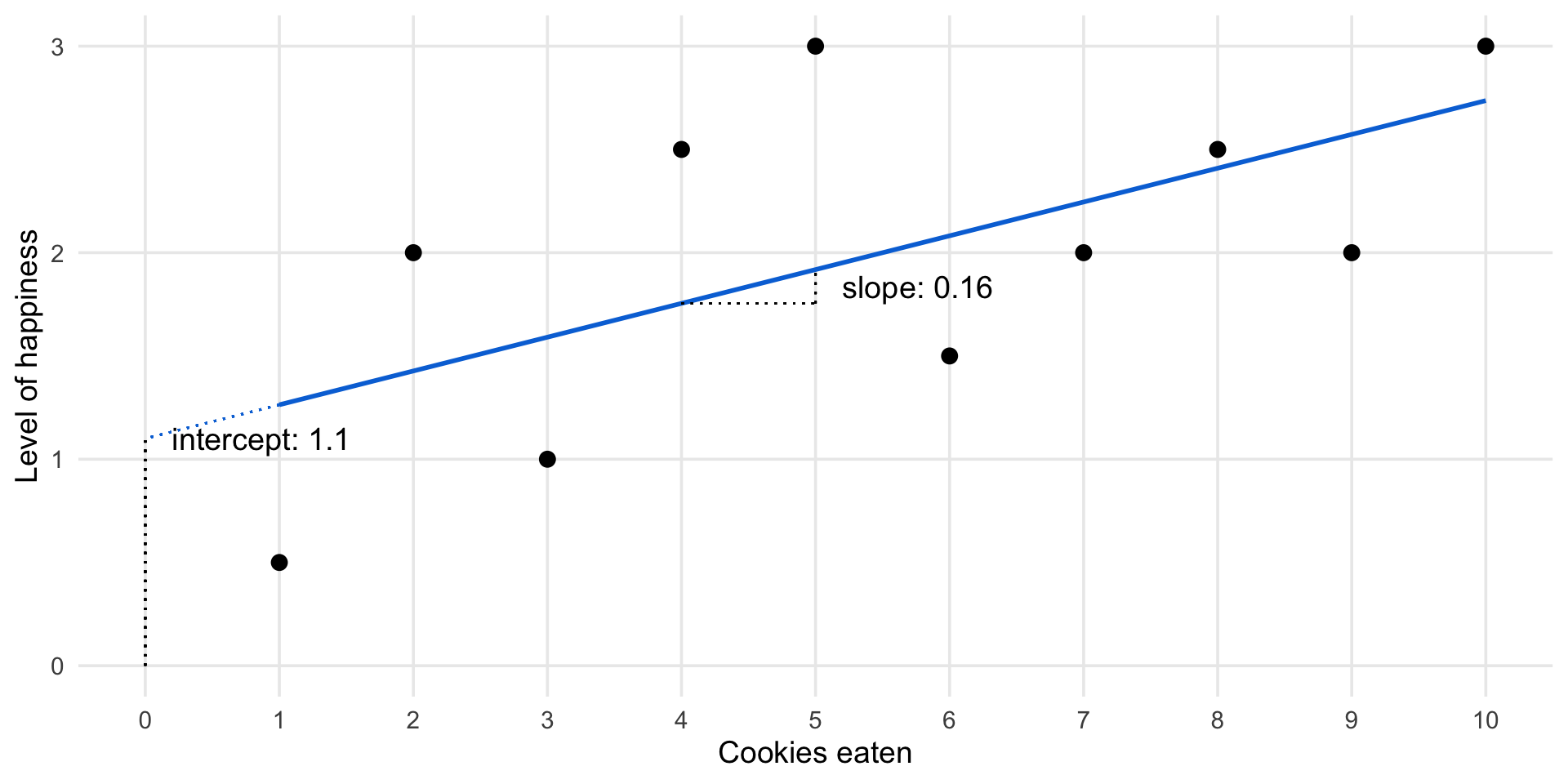
We get some more detail doing this:

# Compute the OLS regression model
ols_model <- lm(happiness ~ cookies, data = cookies)

summary(ols_model)

Call:
lm(formula = happiness ~ cookies, data = cookies)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.76364 -0.57955 -0.07727  0.49545  1.08182 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)  
(Intercept)  1.10000    0.47025   2.339   0.0475 *
cookies      0.16364    0.07579   2.159   0.0629 .
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.6884 on 8 degrees of freedom
Multiple R-squared:  0.3682,    Adjusted R-squared:  0.2892 
F-statistic: 4.662 on 1 and 8 DF,  p-value: 0.06287

Interpreting linear regression output

“A one unit increase in X is associated with a beta 1 increase (or decrease) in Y, on average.”

We can also store the output in a data frame directly using the broom package.

library(broom)

tidy(ols_model)

# A tibble: 2 × 5
  term        estimate std.error statistic p.value
  <chr>          <dbl>     <dbl>     <dbl>   <dbl>
1 (Intercept)    1.1      0.470       2.34  0.0475
2 cookies        0.164    0.0758      2.16  0.0629

Statistical Inference for Linear Regression

How does hypothesis testing work for linear regression?

• Everything we’ve learned so far on hypothesis testing and statistical power also applies to linear regression

• In the last two sessions, our estimate was the difference between comedies and action movies.

• This time, our estimate is the slope of the regression.

Simulate a cookies and happiness population

Let’s simulate a true effect world of cookie data with.

set.seed(1234) # For reproducibility

# true happiness without any cookies
intercept <- 1

# effect of one cookie on happiness
slope <- 0.3

imaginary_cookies <- tibble(
  id = 1:1000000,
  cookies = sample(seq(1, 10, by = 1), size = 1000000, replace = TRUE),
  # the rnorm() function adds noise, i.e. some random error
  happiness = intercept + slope * cookies + rnorm(length(cookies), mean = 0, sd = 0.5)
)

Generate a sampling distribution

Imagine we can ask a sample of 10 people on how happy they are and how many cookies they eat a day - let’s draw many (1000) samples of 10 people and calculate a regression for each.

n_simulations <- 1000
regression_estimates <- c() # make an empty vector
sample_size <- 10

for (i in 1:n_simulations) {
  # draw a sample of 10 people
  imaginary_sample <- imaginary_cookies |> 
    sample_n(sample_size)
  
  # run a regression on the sample 
  estimate <- lm(happiness ~ cookies, data = imaginary_sample) |> 
    tidy() |> 
    filter(term == "cookies") |> 
    pull(estimate)

  regression_estimates [i] <- estimate
}

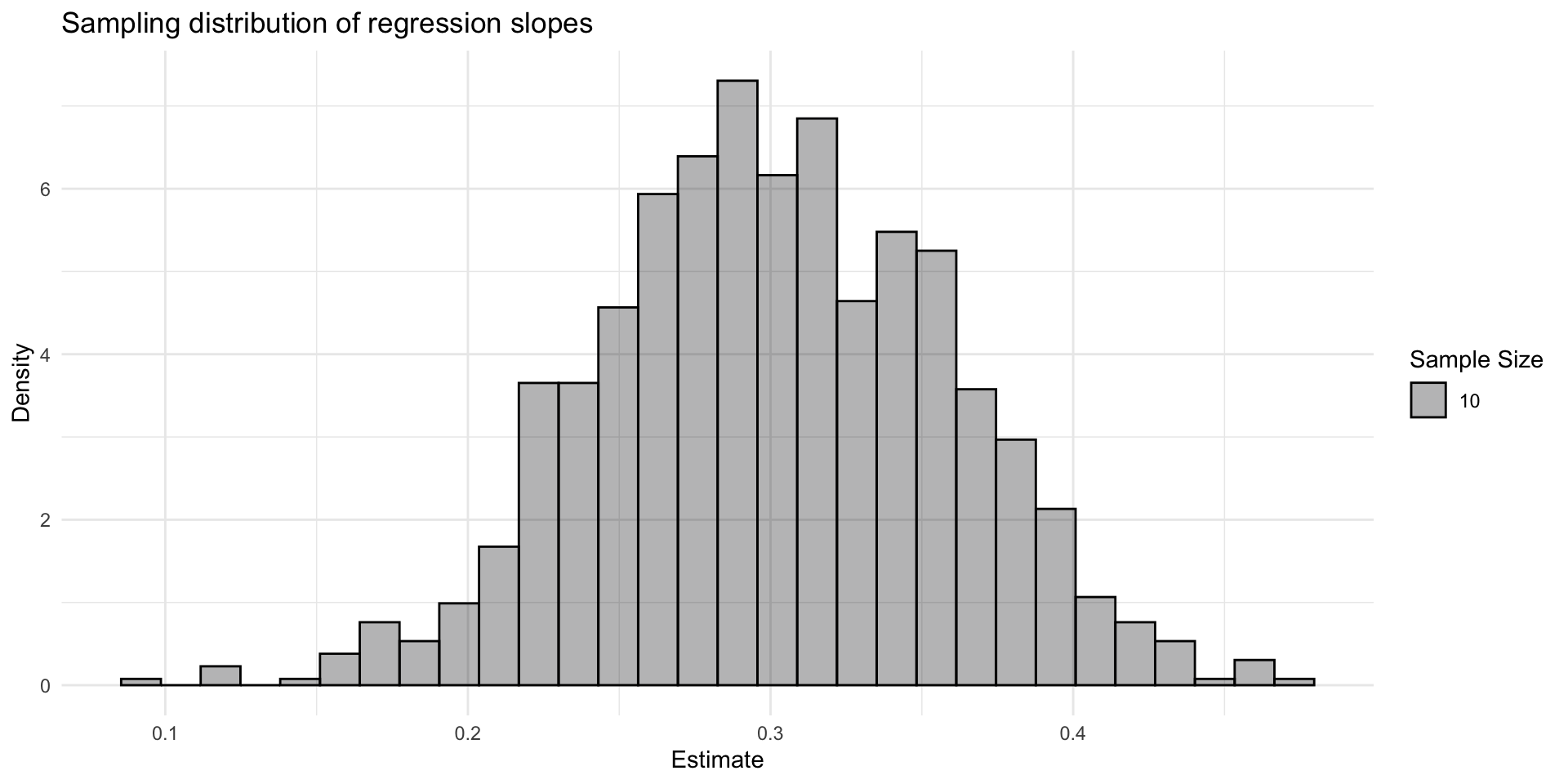
According to the Central Limit Theorem, what do we expect the sampling distribution to look like?

Sampling distribution

1. The sampling distribution of estimates approximates a normal distribution.

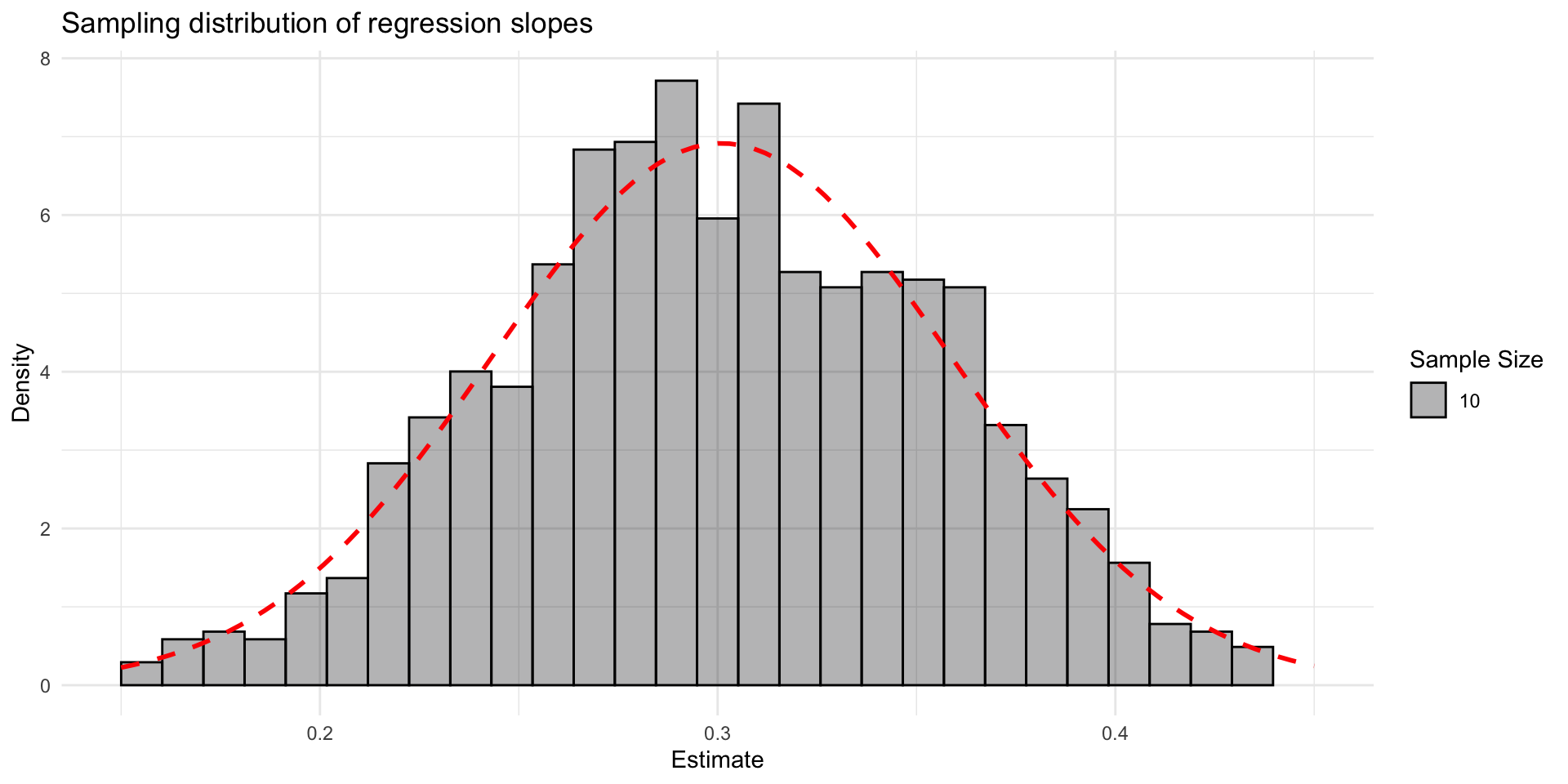
Sampling distribution

2. The sampling distribution gets narrower with a larger sample size

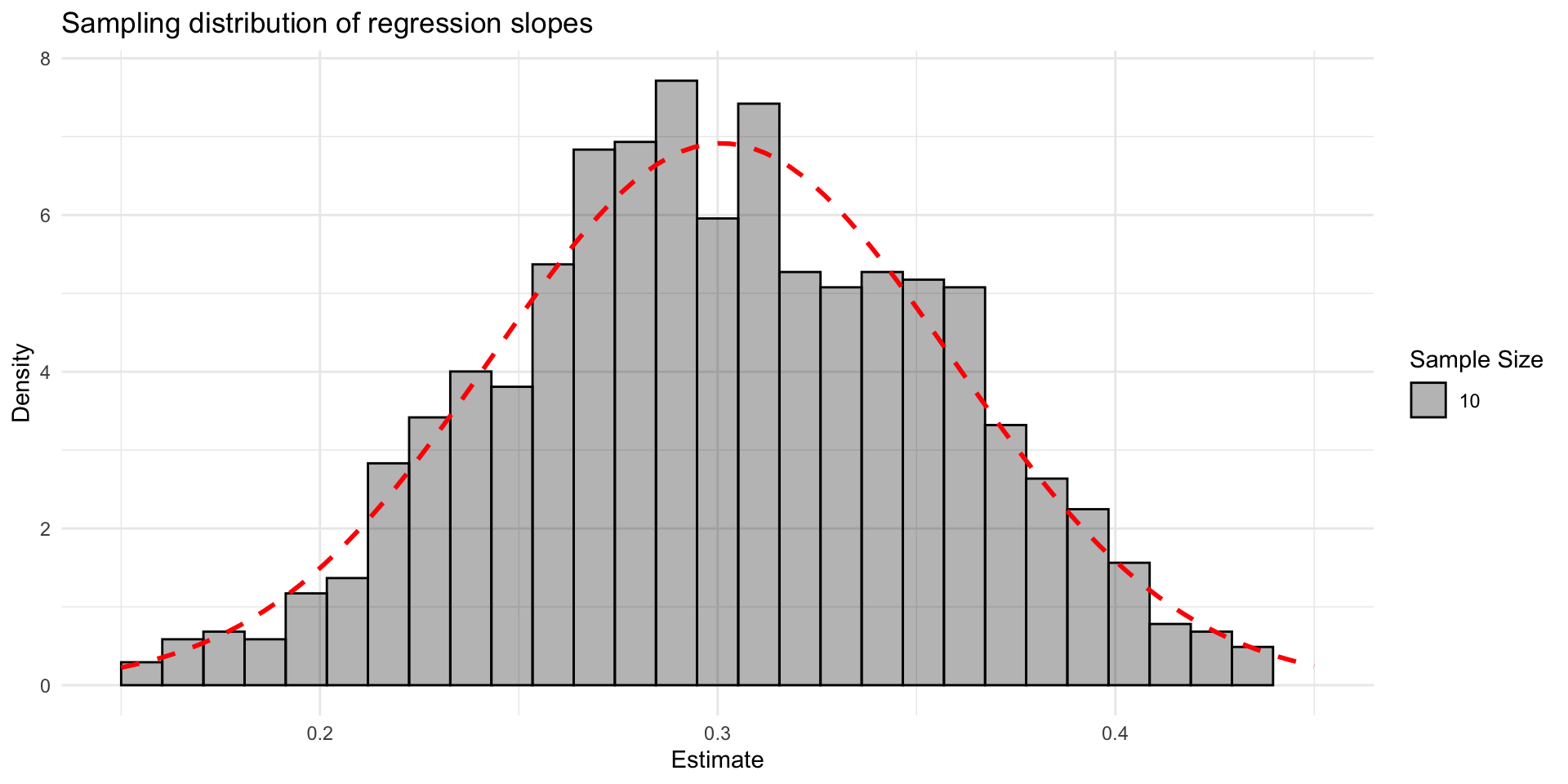
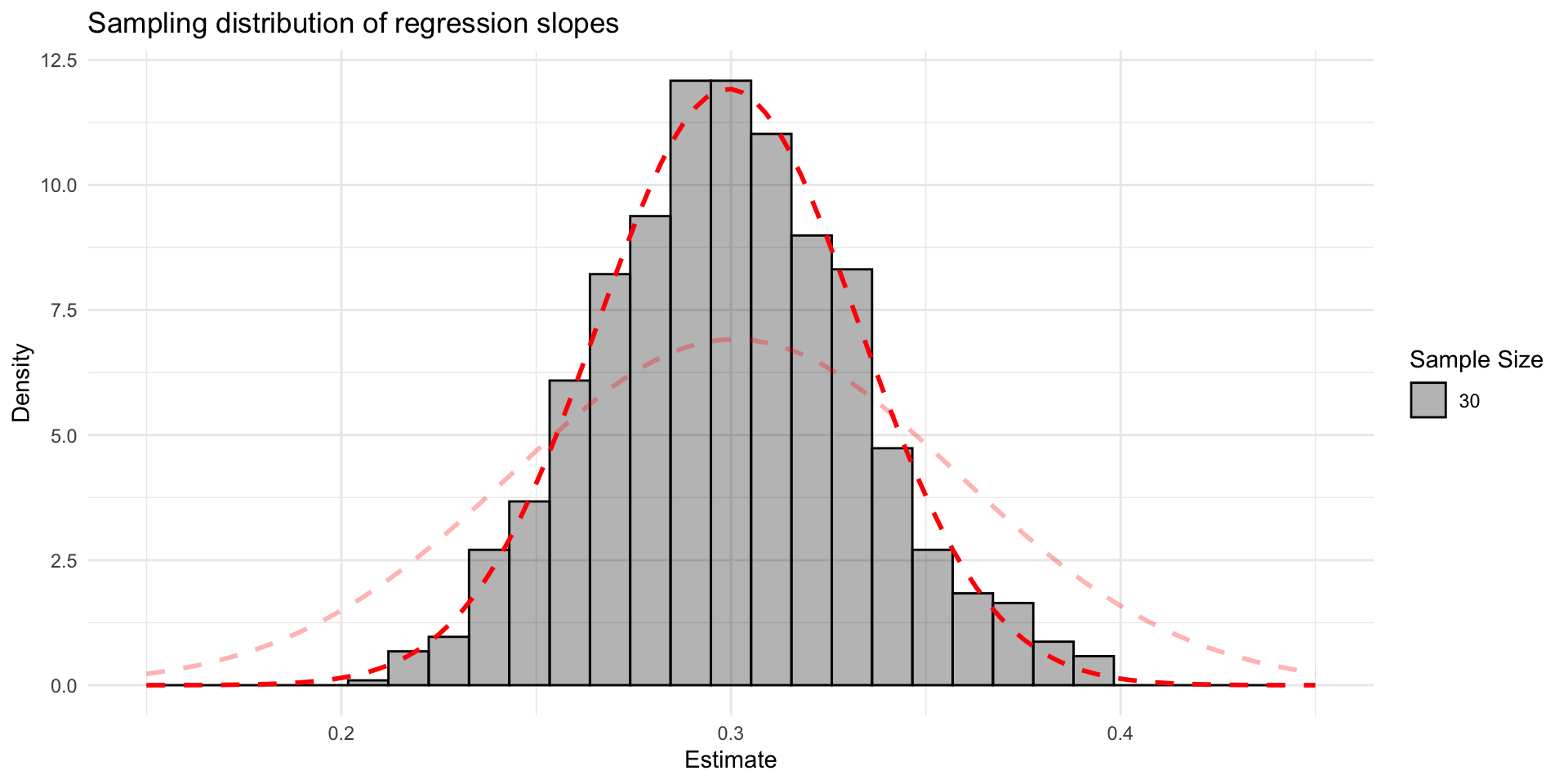
Sampling distribution

2. The sampling distribution gets narrower with a larger sample size

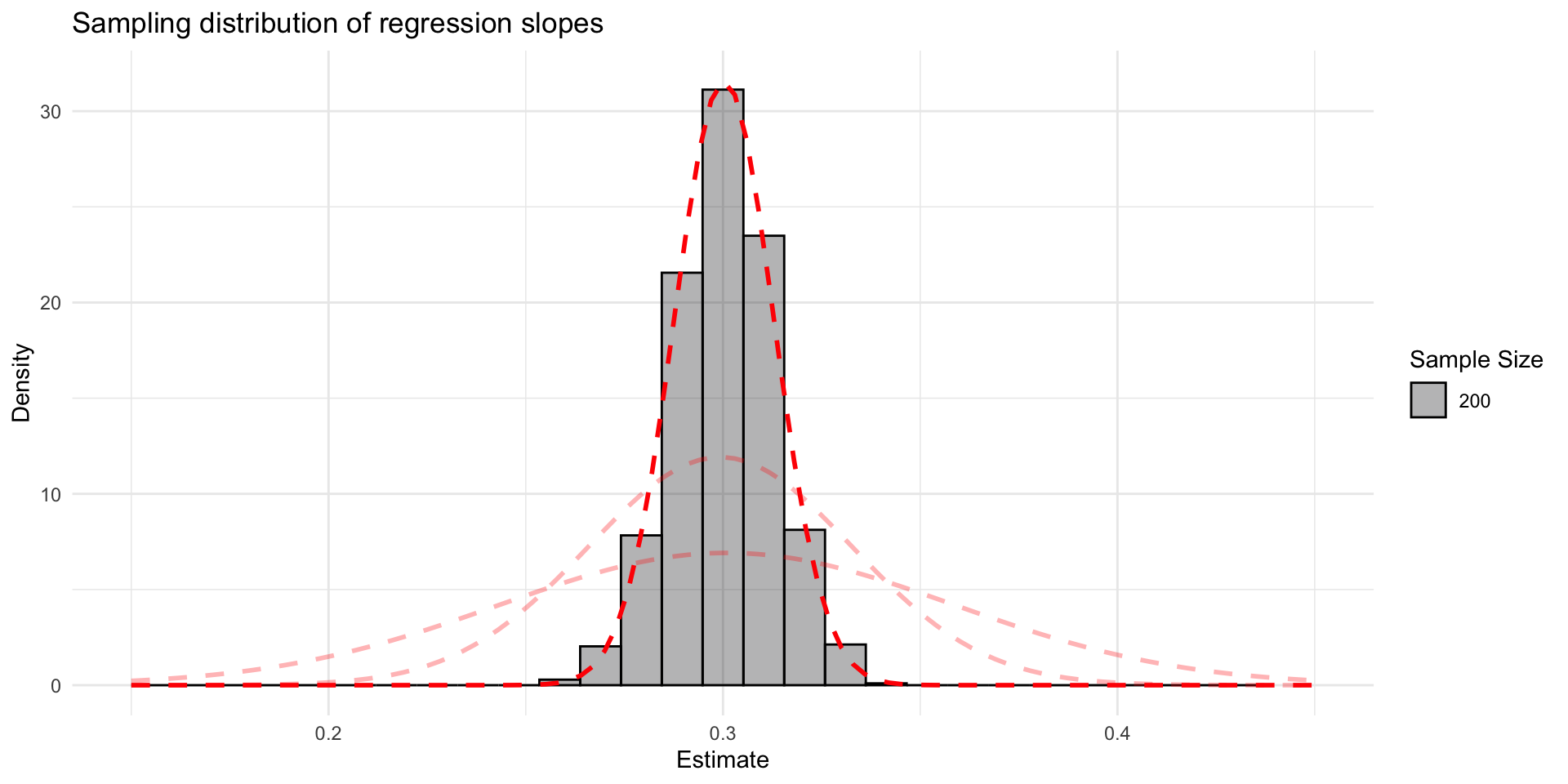
Your turn: A power simulation for a regression analysis

Imagine we want to run a study to measure the association between cookies and happiness.

We want to know how many participants we need to recruit to achieve a statistical power of 0.8, assuming an effect of 0.1.

The final output should be a graph with the power for different sample sizes.

Note

This task is definitely a challenge. It’s ok to get stuck. Make sure to use the guide on power simulation on the course website, and build on the functions on the next slides.

15:00

Your turn: A power simulation for a regression analysis

generate_sample <- function(sample_size){
  
  # set regression parameters
  intercept <- 1
  slope <- 0.1
  
  sample <- tibble(
    id = 1: sample_size,
    cookies = sample(seq(1, 10, by = 1), size = sample_size, replace = TRUE),
    # the rnorm() function adds noise, i.e. some random error
    happiness = intercept + slope * cookies + rnorm(length(cookies), mean = 0, sd = 1)
  )
  
  return(sample)
}

# test
# generate_sample(sample_size = 100)

Your turn: A power simulation for a regression analysis

calculate_regression <- function(sample){
  
  # run a regression on the sample 
  p.value <- lm(happiness ~ cookies, data = sample) |> 
    tidy() |> 
    filter(term == "cookies") |> 
    pull(p.value)
  
  return(p.value)
}

# test
# test_sample <- generate_sample(sample_size = 100)
# calculate_regression(sample = test_sample)

Your turn: A power simulation for a regression analysis

generate_samples <- function(n_simulations, sample_size) {
  
  # Make an empty vector
  p.values <- numeric(n_simulations)
  
  for (i in 1:n_simulations) {
    # Draw a sample with the specified size
    sample <- generate_sample(sample_size) 
    
    # Get an estimate
    p.values[i] <-  calculate_regression(sample)
  }
  
  return(p.values)
}
# test
# generate_samples(n_simulations = 100, sample_size = 10)

Solution

First, we need a function to calculate power

calculate_power <- function(p.values){
  
  # get statistical power 
  power <- data.frame(p.values) |> 
    mutate(significant = ifelse(p.values <= 0.5, TRUE, FALSE)) |> 
    summarize(share_significant = sum(significant) / n()) |> 
    pull(share_significant)
  
  return(power)
}
# test
# some_p.values <- generate_samples(n_simulations = 100, sample_size = 10)
# calculate_power(p.values = some_p.values)

Solution

We can then put it all together in a power simulation function. This function generates 1000 samples, calculates the p-value for the analysis on each sample, and calculates the power.

power_simulation <- function(sample_size, n_simulations = 1000) {
  
  # Generate multiple samples and compute estimates
  sampled_p.values <- generate_samples(n_simulations, sample_size)
  
  # Calculate statistical power
  power <- calculate_power(sampled_p.values)
  
  # Return results
  return(tibble(
    sample_size = sample_size,
    n_simulations = n_simulations,
    estimated_power = power
  ))
}
# test
# power_simulation(sample_size = 30, n_simulations = 100)

Solution

Finally we can use the function to run a power analysis for different sample sizes

sample_sizes <- c(10, 30, 50, 200)

# make an empty data frame
power_data <- tibble()

for (i in sample_sizes) {
  # run power simulation
  power <- power_simulation(sample_size = i, n_simulations = 1000)
  
  power_data <- bind_rows(power_data, power)
}

Solution

We can then plot the power curve

ggplot(power_data, 
       aes(x = sample_size, y = estimated_power)) +
  geom_point(color = 'red', size = 1.5) +
  geom_line(color = 'red', size = 1) + 
  # add a horizontal line at 80%
  geom_hline(aes(yintercept = .8), linetype = 'dashed') + 
  # Prettify!
  theme_minimal() + 
  scale_y_continuous(labels = scales::percent, limits = c(0,1)) + 
  labs(title = "Power Simulation for the effect of Cookies on Happiness",
       x = 'Sample Size', y = 'Power')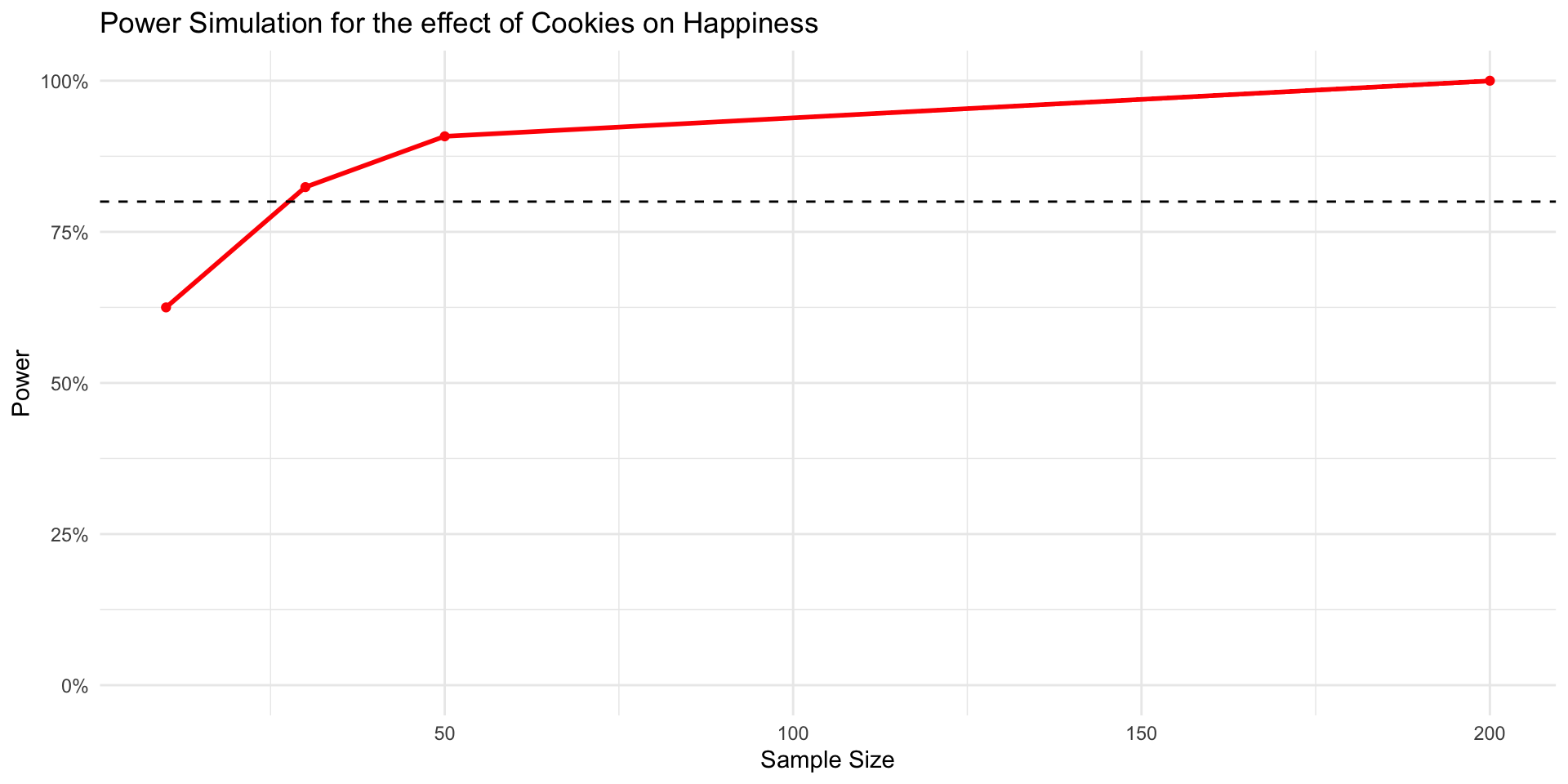

That’s it for today :)