Scientific Publishing and the Replication Crisis

Overview

1. On the whole science works

2. Replication Crisis

3. Reproducibility

4. Replicability

   • P-Hacking
   • File-drawer effect

5. How to do better science?
   • Reproducible manuscripts
   • Preregistrations

On the whole science works

If I have seen further than others,

it is by standing upon the shoulders

of giants.
— Isaac Newton

Science is cumulative

• Researchers build on each others findings

• This way, science is self correcting: If something doesn’t doesn’t turn out to be right, (at some point) other researchers will notice

(A typical textbook) pyramid of evidence

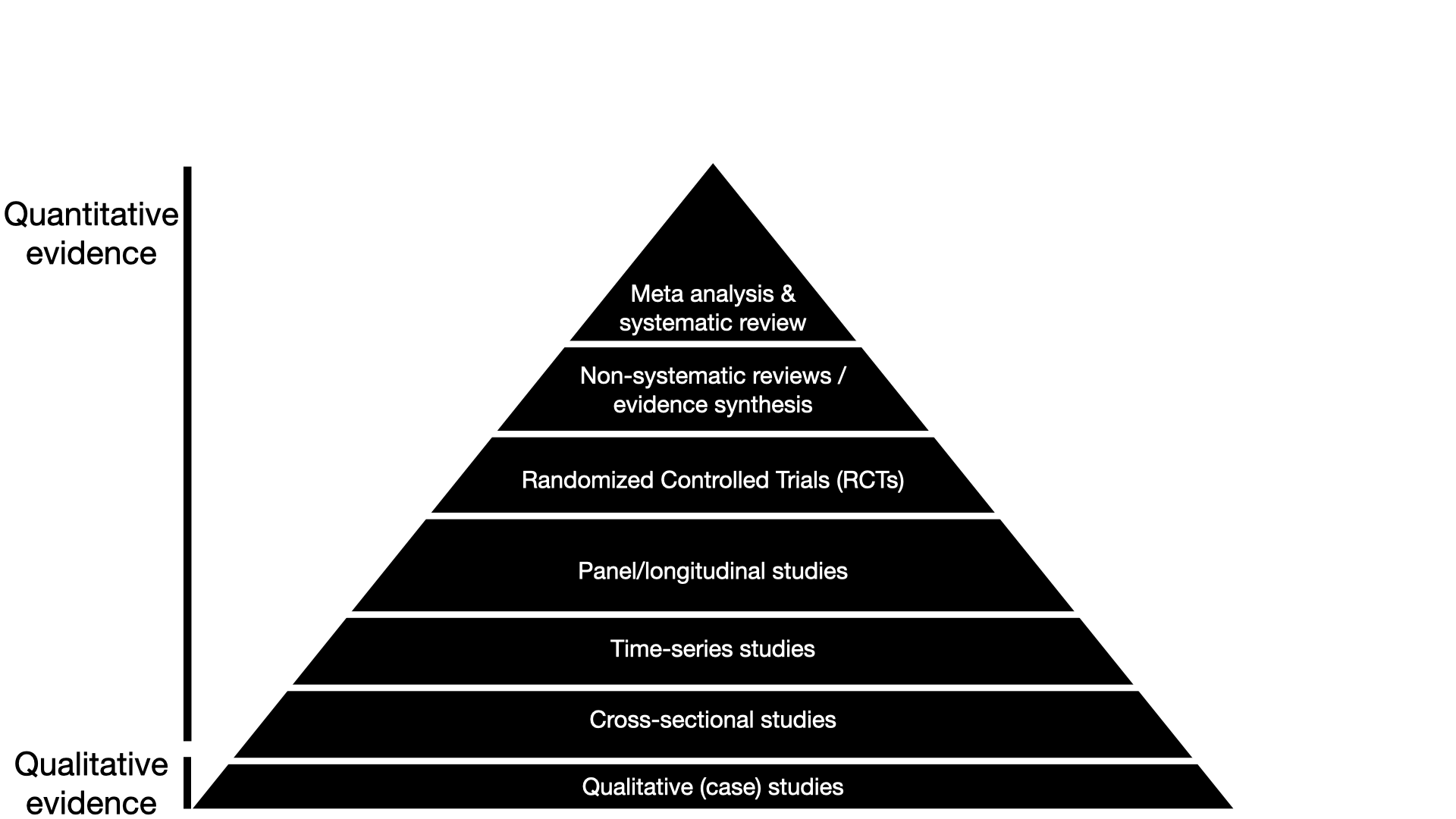
… but as great as science often is, it has some issues, and some are very structural

The replication Crisis

Reproducibility

When scientists can obtain the results of other scientists…

… using the same data and following the same methods

Would this ever not be the case?

Unfortunately, yes!

Oza, A. (2023). Reproducibility trial: 246 biologists get different results from same data sets. Nature.

Replicability

When scientists can obtain the results of other scientists…

… collecting new data, following the same methods

OPEN SCIENCE COLLABORATION. (2015). Estimating the reproducibility of psychological science. Science.

Confusing!

The paper uses the word “reproducibility”, but in fact they replicated studies.

That is, they collected new data.

What has gone wrong? Is science a big fraud?

No! Fraud in science does happen, but it’s rare.

There are two main issues:

1. P-hacking

2. File-drawer effect

Your turn: P-hacking

Imagine you had run a fictional experiment (download the data here: imaginary_beatle_experiment.csv or from this week’s content page) to test whether listening to certain music affects people’s behavior or how they perceive themselves. In this fictional experiment, participants were randomly assigned to either:

• Treatment group: Listened to “When I’m Sixty-Four” by The Beatles.

• Control group: Listened to an instrumental jazz piece of similar length.

Afterwards, participants completed a battery of self-report measures and cognitive tasks.

Explore the dataset and look for any evidence that listening to “When I’m 64” had a significant effect on participants (tip, run regressions, you can even add covariates, look only at a subgroup of the data etc.)

10:00

Solution

# You could have tried for example to run this
model <- lm(actual_age ~ condition, data = imaginary_beatle_experiment)

summary(model)

Call:
lm(formula = actual_age ~ condition, data = imaginary_beatle_experiment)

Residuals:
   Min     1Q Median     3Q    Max 
-9.675 -3.043  0.325  2.325  9.957 

Coefficients:
                 Estimate Std. Error t value Pr(>|t|)    
(Intercept)       25.6750     0.4665   55.04   <2e-16 ***
conditionControl  -1.6321     0.6829   -2.39   0.0181 *  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 4.172 on 148 degrees of freedom
Multiple R-squared:  0.03717,   Adjusted R-squared:  0.03066 
F-statistic: 5.713 on 1 and 148 DF,  p-value: 0.0181

A significant difference! But completely implausible.

Solution

This is how the data was generated:

# a function to simulate the data
simulate_phacking_data <- function(n = 150) {
  tibble(
    id = 1:n,
    # simulate the experimental manipulation
    condition = sample(c("Beatles", "Control"), n, replace = TRUE),
    # all variables below are generate completely independently of the manipulation
    actual_age = round(rnorm(n, mean = 25, sd = 4)),
    gender = sample(c("Male", "Female", "Other"), n, replace = TRUE, prob = c(0.45, 0.45, 0.1)),
    political_orientation = sample(1:7, n, replace = TRUE),
    height_cm = round(rnorm(n, mean = 170, sd = 10)),
    reaction_time_ms = round(rlnorm(n, meanlog = 6.5, sdlog = 0.3)),
    mood_score = round(rnorm(n, mean = 5, sd = 1.5), 1),
    memory_score = round(rnorm(n, mean = 10, sd = 3)),
    confidence = sample(1:7, n, replace = TRUE),
    perceived_age = actual_age + rnorm(n, mean = 0, sd = 2),
    stress_level = round(rnorm(n, mean = 4, sd = 1.5), 1),
    sleep_hours = round(rnorm(n, mean = 7, sd = 1.2), 1),
    caffeine_intake_mg = round(rnorm(n, mean = 200, sd = 75)),
    exercise_minutes = round(rnorm(n, mean = 30, sd = 15)),
    social_media_minutes = round(rnorm(n, mean = 90, sd = 40)),
    screen_time_hours = round(rnorm(n, mean = 5, sd = 2), 1)
  )
}

No true effect on any other variable.

Solution

And this is how the sample was picked:

# simulate until a data set returns a treatment 
# effect on actual age of participants

set.seed(13487)

# Simulate multiple datasets and "p-hack" until p < .05
find_false_positive <- function(n = 10, max_tries = 10000) {
  for (i in 1:max_tries) {
    data <- simulate_phacking_data(n)
    model <- lm(actual_age ~ condition, data = data)
    p_val <- tidy(model) |> 
      filter(term == "conditionControl") |> 
      pull(p.value)
    
    if (p_val < 0.05) {
      cat("🔎 Found significant p =", round(p_val, 4), "on try", i, "\n")
      return(data)
    }
  }
  stop("❌ No significant result found within max_tries.")
}

# Example: Find a "lucky" false positive dataset
imaginary_beatley_experiment <- find_false_positive(n = 150)

Re-sample until–by chance–a significant result pops up.

P-Hacking

Remember a p-value:

It’s the probability of observing an estimate at least as extreme as the one in our sample, in a world where there is no true effect (the Null world).

Remember statistical significance:

If p-value < 5% (arbitrary threshold)

We accept a 5% chance that our results could have occurred in a Null world.

P-Hacking

That means:

In a world where there is no effect, in 5% of (or 1 out of 20) samples, we find a false positive.

If we look at a different outcome variable, that’s basically taking a new sample.

If we measure 20 outcomes, in a world where there is no effect, we would expect 1 to yield a statistically significant effect.

• To Illustrate how easy p-hacking is, the authors ran an RCT.

• They found that listening to the classic Beatles song “When I’m Sixty-Four” makes people younger

(Yes, it literally reversed time)

• All analysis were using sound statistical methods and randomization

How did they achieve it?

• Just like you in the exercise: p-hacking
• They collected information about a number of characteristics of their study subjects, and then controlled for one that happened to give them the result they were looking at. (The age of the subject’s father).
• They also continued the experiment until they got a significant result, rather than predetermining the sample size.

File-drawer effect

Illustration from Calling Bullshit

Researchers are incentives to publish positive, statistically significant results.

But this can result faulty images of the evidence.

How bad is the issue?

Ioannidis, J. P. A. (2005). Why Most Published Research Findings Are False. PLoS Medicine.

Let’s take a step back

Assume that we have a “total Null world” (no true effect for no study in science)

	H₀ True (100%)
Significant Finding (Positive result) α = 5%, 1−β = 80%	False Positive 5%
Non-Significant Finding (Negative result) 1−α = 95%, β = 20%	True Negative 95%

Let’s take a step back

Now assume we live in a “total True world” (only true effects in all of science)

	H₀ True (0%)	H₁ True (100%)
Significant Finding (Positive result) α = 5%, 1−β = 80%	0%	True Positive 80%
Non-Significant Finding (Negative result) 1−α = 95%, β = 20%	0%	False Negative 20%

Now let’s assume a world where half of science tests true effects

For illustration, let’s assume science consists of n = 200 studies

	H₀ True (50%)	H₁ True (50%)
Significant Finding (Positive result) α = 5%, 1−β = 80%	False Positive 5% × 50% = 2.5% (5 studies)	True Positive 80% × 50% = 40% (80 studies)
Non-Significant Finding (Negative result) 1−α = 95%, β = 20%	True Negative 95% × 50% = 47.5% (95 studies)	False Negative 20% × 50% = 10% (20 studies)

And now let’s assume a world where only 5% of science tests true effects

In other words, we assume scientists generally test implausible hypotheses

	\(H_0\) True (95%)	\(H_1\) True (5%)
Significant Finding (Positive result) \(\alpha = 5\%, 1-\beta = 80\%\)	False Positive 5% × 95% = 4.75% (9.5 studies)	True Positive 80% × 5% = 4% (8 studies)
Non-Significant Finding (Negative result) \(1-\alpha = 95\%, \beta = 20\%\)	True Negative 95% × 95% = 90.25% (180.5 studies)	False Negative 20% × 5% = 1% (2 studies)

We never know the ratio of true vs. null effects in science…

…but what we would like to know is:

Given that we observe a statistically significant effect, what’s the probability that it is true?

Positive Predictive Value (PPV)

\[ \text{PPV} = \frac{\text{True Positives}}{\text{True Positives} + \text{False Positives}} = \frac{8}{8 + 9.5} = \frac{8}{17.5} \approx 45.7\% \]

	\(H_0\) True (95%)	\(H_1\) True (5%)
Significant Finding (Positive result) \(\alpha = 5\%, 1-\beta = 80\%\)	False Positive 5% × 95% = 4.75% (9.5 studies)	True Positive 80% × 5% = 4% (8 studies)
Non-Significant Finding (Negative result) \(1-\alpha = 95\%, \beta = 20\%\)	True Negative 95% × 95% = 90.25% (180.5 studies)	False Negative 20% × 5% = 1% (2 studies)

This is Ioannidis’ argument:

If we assume that

• scientists test implausible hypotheses

• and that only a fraction of negative results gets reported

then most of research findings are wrong (i.e. low PPV).

This is likely an overestimation of the problem!

One can argue with Ioannidis’ assumptions.

Also, the paper is old (2005), and many things have changed for the better since.

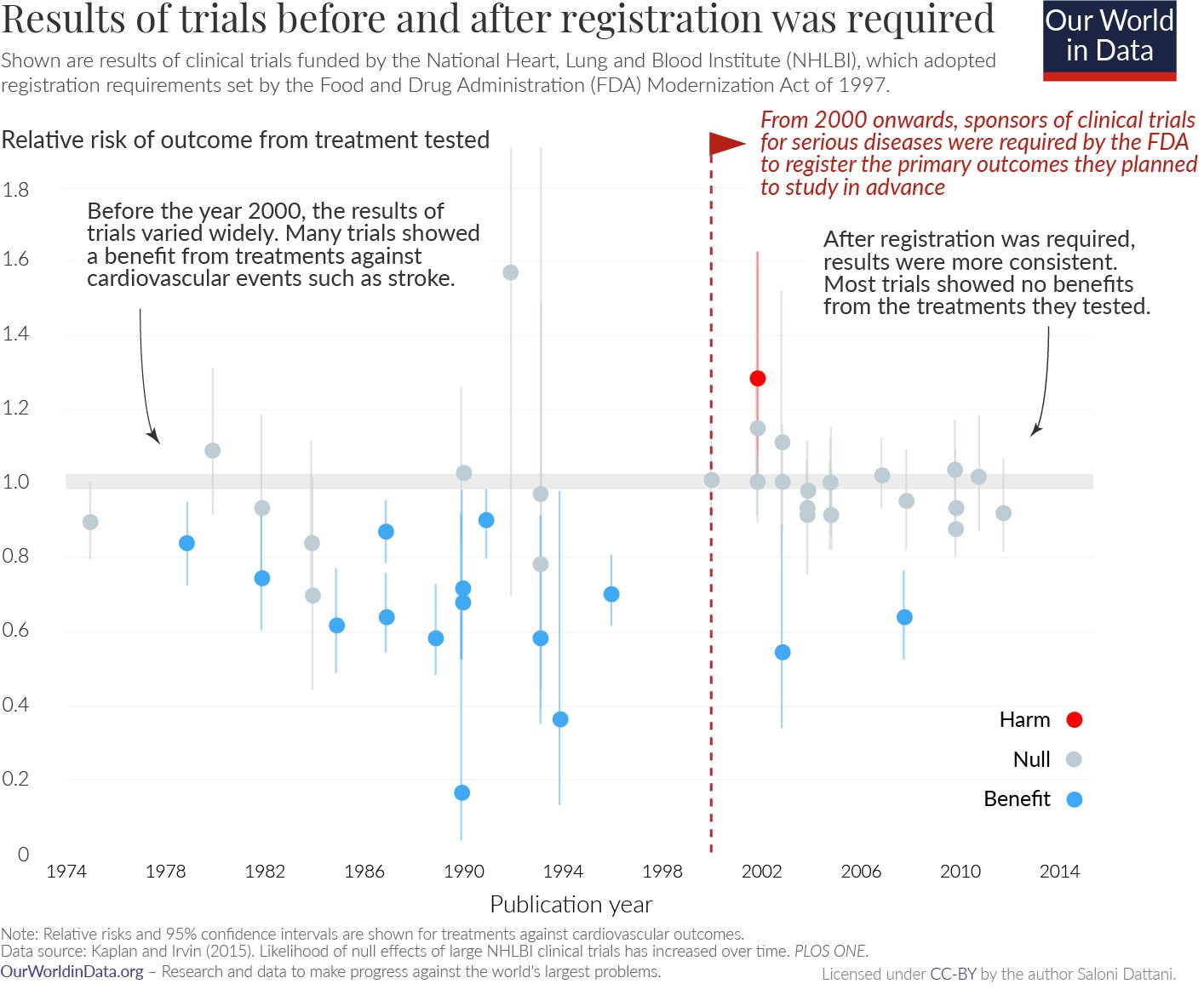
US Food and Drug Administration (FDA)

• In the United States clinical trials (experiments using human subjects to test outcomes of medical treatments) are required by law to register this trial with the FDA

• This involves explaining what the trial is designed to test, how the trial will be conducted, and how the outcomes will be measured.

• Once the trial is completed, the researchers are also required to report the results to the FDA.

• However, they are not required to publish the results in a scientific journal.

Turner, E. H., Matthews, A. M., Linardatos, E., Tell, R. A., & Rosenthal, R. (2008). Selective Publication of Antidepressant Trials and Its Influence on Apparent Efficacy. New England Journal of Medicine.

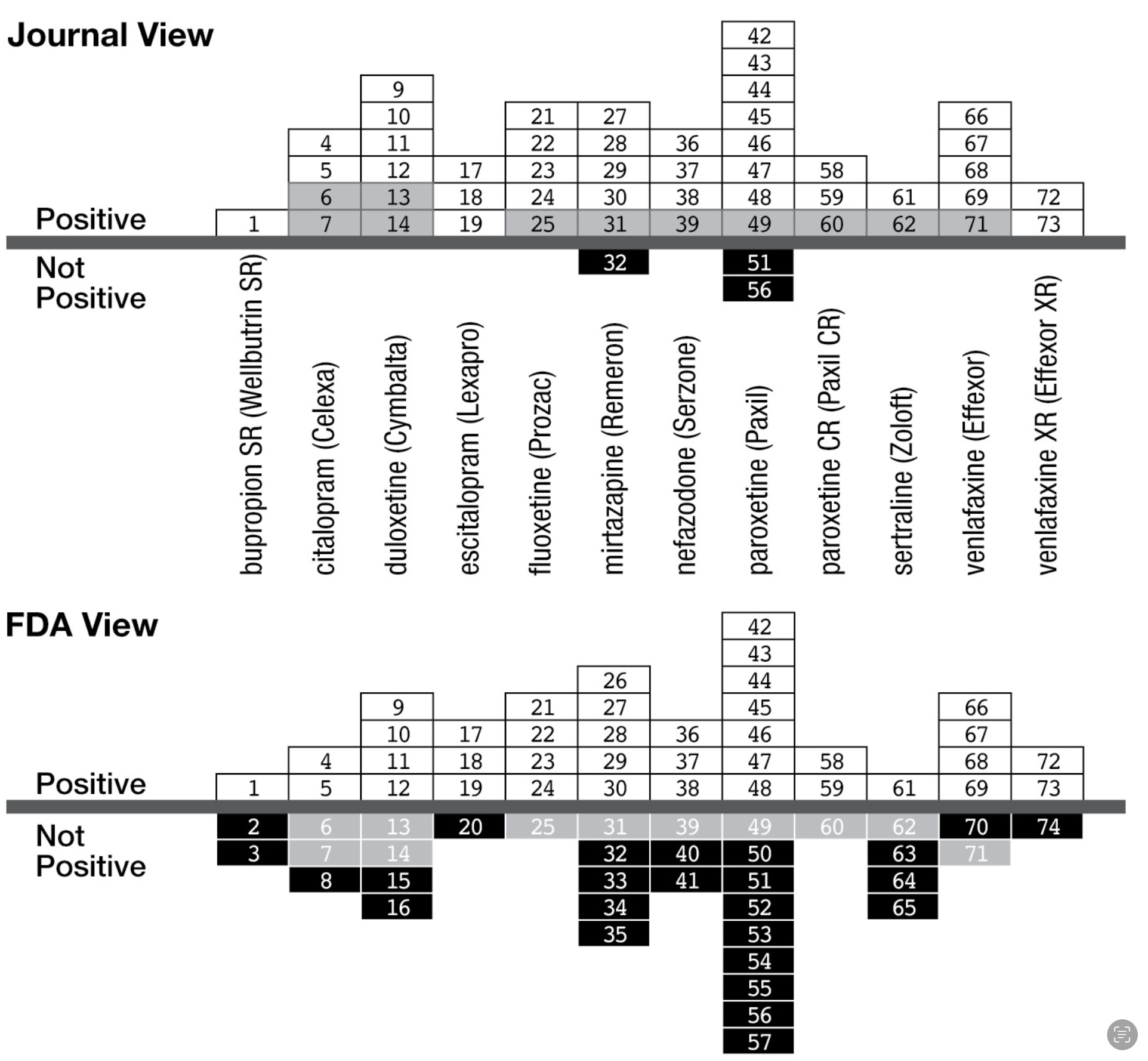
Illustration from Bergstrom, C. T., & West, J. D. (2020). Calling bullshit: The art of skepticism in a data-driven world (First edition). Random House.

How to do better science?

Two main solutions

1. At the least, make data and code public

(at best, write reproducible manuscripts)

This is something you’ve learned by using Quarto! 🎉

Two main solutions

1. At the least, make data and code public

(at best, write reproducible manuscripts)

2. Preregister studies

Pre-registration in a nutshell

A time-stamped document describing the details of the planned study

Benefits:

• makes research process more transparent

• allows to clearly distinguish a priori and post-hoc decisions

• makes it harder to fool (the researchers themselve and others)

How exactly does it work?

There are different options but the most common one is to use the Open Science Framework (OSF)

• large number of templates

• all participating authors get informed and can cancel within 48h

• prereg can be kept privat for a while (if needed to protect the project)

What goes into a preregistration?

Anything that might be considered a researcher degree of freedom

• fixed decisions (e.g. the research design, outcome measures)

• decision rules (e.g. “if we cannot collect 100 participants until June 5 2025, we will stop the data collection that very day and…”)

• statistical models (ideally analysis scripts, including data-dependent decision rules)

• sample size and power analysis

From Dattani, S. (2022). Why randomized controlled trials matter and the procedures that strengthen them. Our World in Data.

Two main solutions

1. At the least, make data and code public

(at best, write reproducible manuscripts)

2. Preregister studies

3. Change the scientific publishing system

Registered reports

Illustration from the OSF

• journals commit to publishing results, no matter whether significant or not

• relevance of a study is determined based on the research question, not the result

Scheel, A. M., Schijen, M. R. M. J., & Lakens, D. (2021). An Excess of Positive Results: Comparing the Standard Psychology Literature With Registered Reports. Advances in Methods and Practices in Psychological Science.

That’s it for today :)