Meta Analyses

Overview

  1. Why meta-analyses

  2. The research question

  3. Effect Sizes

  4. Systematic literature search

  5. Running a meta-analysis

Why meta-analyses?

(A typical textbook) pyramid of evidence

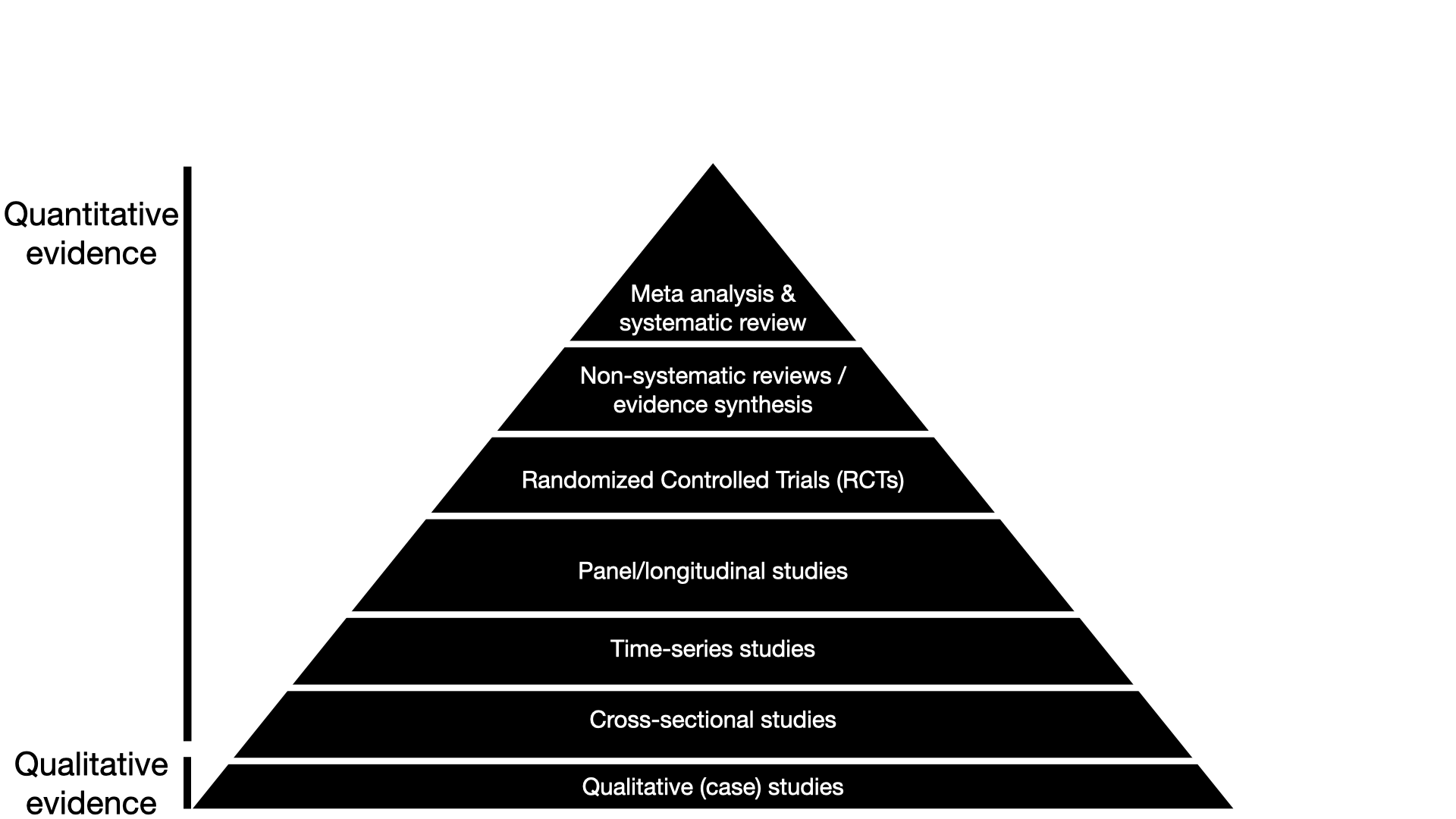
Why are meta-analyses at the top of the pyramid?

  • Results of single studies are affected by many factors:

    • the country
    • experimental setup
    • researchers
    • sample demographics…

  • Averaging across many studies, we get a more robust, generalizable result

The research question

Case study: “Can people tell true news from false News ?”

Pfänder, J., & Altay, S. (2025). Spotting false news and doubting true news: A systematic review and meta-analysis of news judgements. Nature Human Behaviour, 1–12. https://doi.org/10.1038/s41562-024-02086-1

Case study: “Can people tell true news from false News ?”

Pennycook, G., Binnendyk, J., Newton, C., & Rand, D. G. (2021). A Practical Guide to Doing Behavioral Research on Fake News and Misinformation. Collabra: Psychology, 7(1), 25293.

Define a quantifiable outcome



\[ \text{discernment} = \text{mean accuracy}_{\text{true news}} - \text{mean accuracy}_{\text{false news}} \]

Your turn:

  1. Download the data from:

Lyons, B., Modirrousta-Galian, A., Altay, S., & Salovich, N. A. (2024). Reduce blind spots to improve news discernment? Performance feedback reduces overconfidence but does not improve subsequent discernment. https://doi.org/10.31219/osf.io/kgfrb

Lyons_2024.csv

  1. Calculate a discernment score
05:00

Solution

lyons |> 
  group_by(veracity) |> 
  summarize(mean = mean(accuracy, na.rm = TRUE)) |> 
  pivot_wider(names_from = veracity, 
              values_from = mean) |> 
  mutate(discernment = true - fake)
# A tibble: 1 × 3
   fake  true discernment
  <dbl> <dbl>       <dbl>
1  1.86  2.56       0.695

Is this score large?

table(lyons$scale)

    4 
10671

The study used a 4-point scale. On this scale, a value of 0.69 seems quite large.

Effect sizes

What are effect sizes?

In Meta-analyses not individual participants, but single studies are the unit of analysis

The outcomes of these studies are called “effect sizes”.

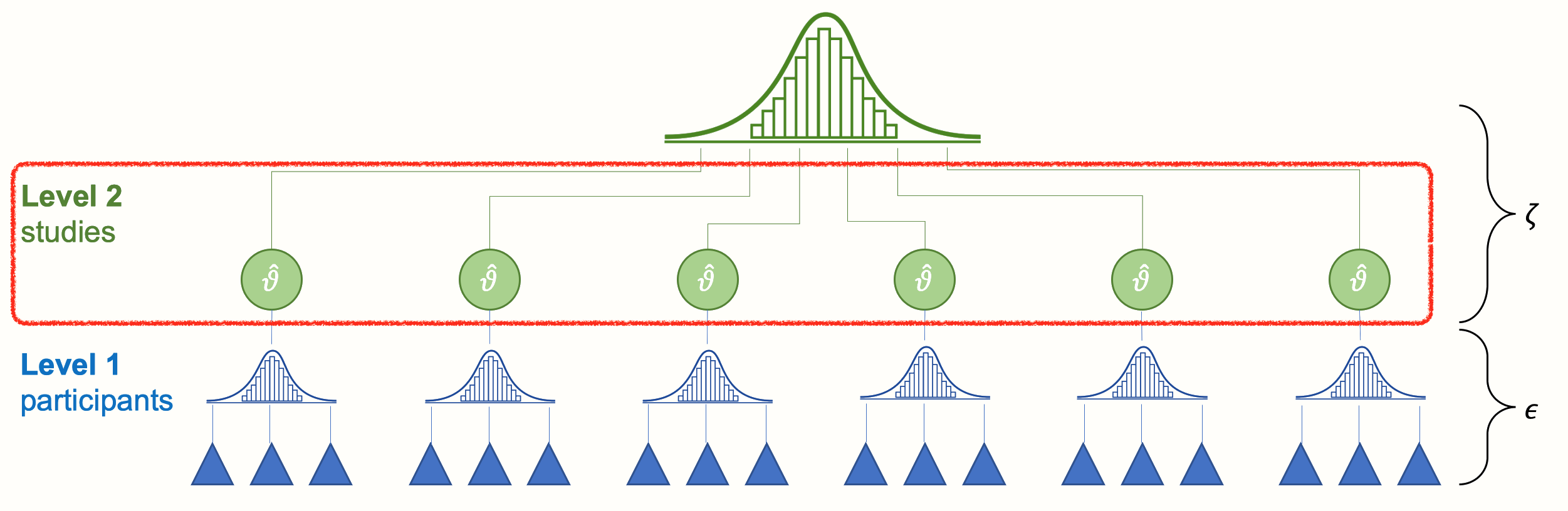
Graphic adapted from: Harrer, M., Cuijpers, P., A, F. T., & Ebert, D. D. (2021). Doing Meta-Analysis With R: A Hands-On Guide (1st ed.). Chapman & Hall/CRC Press.

Your turn:

  1. Download the data from

Allen, J., Arechar, A. A., Pennycook, G., & Rand, D. G. (2021). Scaling up fact-checking using the wisdom of crowds. Science Advances, 7(36), eabf4393.

Allen_2021.csv

  1. Calculate the discernment score.

  2. How does this compare to the other study? What issue are you seeing when you want to compare the two?

05:00

Solution

allen |> 
  group_by(veracity) |> 
  summarize(mean = mean(accuracy, na.rm = TRUE)) |> 
  pivot_wider(names_from = veracity, 
              values_from = mean) |> 
  mutate(discernment = true - fake)
# A tibble: 1 × 3
   fake  true discernment
  <dbl> <dbl>       <dbl>
1  3.82  4.74       0.915

Check the scale

unique(allen$scale)
[1] "7"

The effect size is bigger than the one we found for Lyons 2024, but it is also measured on a broader 7-point scale.

This makes it impossible to immediately compare the effect sizes.

Non-standardized effect sizes


…can only be directly interpreted on their original scales


paper_id scale fake true discernment
Allen_2021 7 3.82 4.74 0.92
Lyons_2024_b 4 1.86 2.56 0.69


This is not great if we want to compare studies.

Standardized effect sizes


… are not dependent on specific scales


They allow us to compare effects across studies that use different outcome measures.

Cohen’s d


  • Perhaps the most popular standardized effect size when comparing two groups on a continuous outcome


  • The idea is to express effect sizes in units of standard deviations

Cohen’s d

  • If we plot the distribution of all individual accuracy ratings, we get something like below (slightly less perfect).

  • Cohen’s d uses the standard devations of these distributions

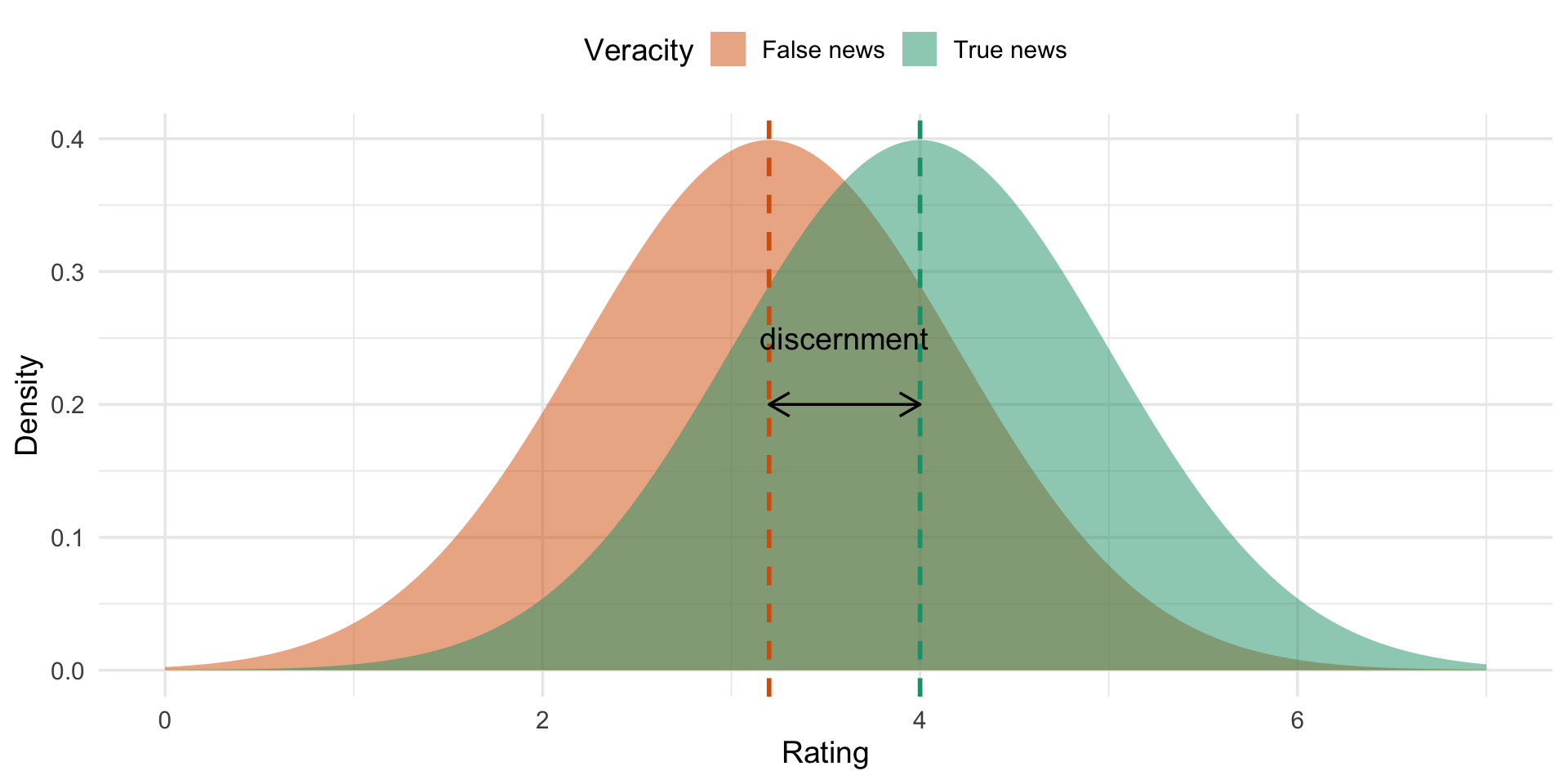
Cohen’s d


\[ \text{Cohen's d} = \frac{\bar{x}_{\text{true}} - \bar{x}_{\text{false}}}{SD_{\text{pooled}}} \]

with

\[ SD_{\text{pooled}} = \sqrt{\frac{SD_{\text{true}}^2+SD_{\text{false}}^2}{2}} \]

Your turn:

In which of the two studies did participants discern better? Calcuate Cohens’ d for the two studies and compare.

05:00

Solution

pooled_sd <- function(sd_true, sd_false) {
  sd_pooled <- sqrt((sd_true^2 + sd_false^2) / 2)
  return(sd_pooled)
}

# Cohen's d for Allen_2021
allen_cohen_d <- allen |> 
  group_by(veracity) |> 
  summarize(mean = mean(accuracy, na.rm = TRUE), 
            sd = sd(accuracy, na.rm = TRUE)) |> 
  pivot_wider(names_from = veracity, 
              values_from = c(mean, sd)) |> 
  mutate(discernment = mean_true - mean_fake, 
         # calculate Cohen's d
         pooled_sd = pooled_sd(sd_true, sd_fake), 
         cohen_d = discernment/pooled_sd
         )

# Cohen's d for Lyons_2024
lyons_cohen_d <- lyons |> 
  group_by(veracity) |> 
  summarize(mean = mean(accuracy, na.rm = TRUE), 
            sd = sd(accuracy, na.rm = TRUE)) |> 
  pivot_wider(names_from = veracity, 
              values_from = c(mean, sd)) |> 
  mutate(discernment = mean_true - mean_fake, 
         # calculate Cohen's d
         pooled_sd = pooled_sd(sd_true, sd_fake), 
         cohen_d = discernment/pooled_sd
         )

# compare
lyons_cohen_d$cohen_d - allen_cohen_d$cohen_d 
[1] 0.2769006

Interpreting Cohen’s d

“Participants in Lyons (2024) discerned better between true and false news than participants in Allen (2021), by 0.28 standard deviations”

Although widely used, this is not always easy to interpret. In psychology, as a rough guide for intepreting Cohen’s d:

  • small (0.2) < medium (0.5) < large (0.8)

(but: depends a lot on the discipline, research question etc.)

If you want to play around with the interpretation of Cohen’s d, check out this guide by Kristoffer Magnusson

Systematic literature review

Tip

  • Literature search something you do before calculating effect sizes, of course.

  • But to do an effective literature search, you need to have an idea of what you are looking for.

  • So, it makes sense to start thinking about the effect size you want to calculate before you do the literature search.

  • In general, we will only very superficially talk about the literature search here.

The search string

Ideally, we want all studies that have ever been written on our research question. The more the better.

But…

Screenshot from a google scholar search on June 27, 2024

We often need to be specific in our search.

The search string


  • When you start a meta-analysis, you often have at least a rough idea of what you are looking for/ have a paper that inspired your idea

  • This gives you ideas of keywords that you could look for.

The search string

This was our search string:

‘“false news” OR “fake news” OR “false stor*” AND “accuracy” OR “discernment” OR “credibilit*” OR “belief” OR “susceptib*”’

Would this search string have yielded a study called “News accuracy ratings of US adults during 2016 presidential elections”?

No, because of how boolean operators work.

Boolean operators

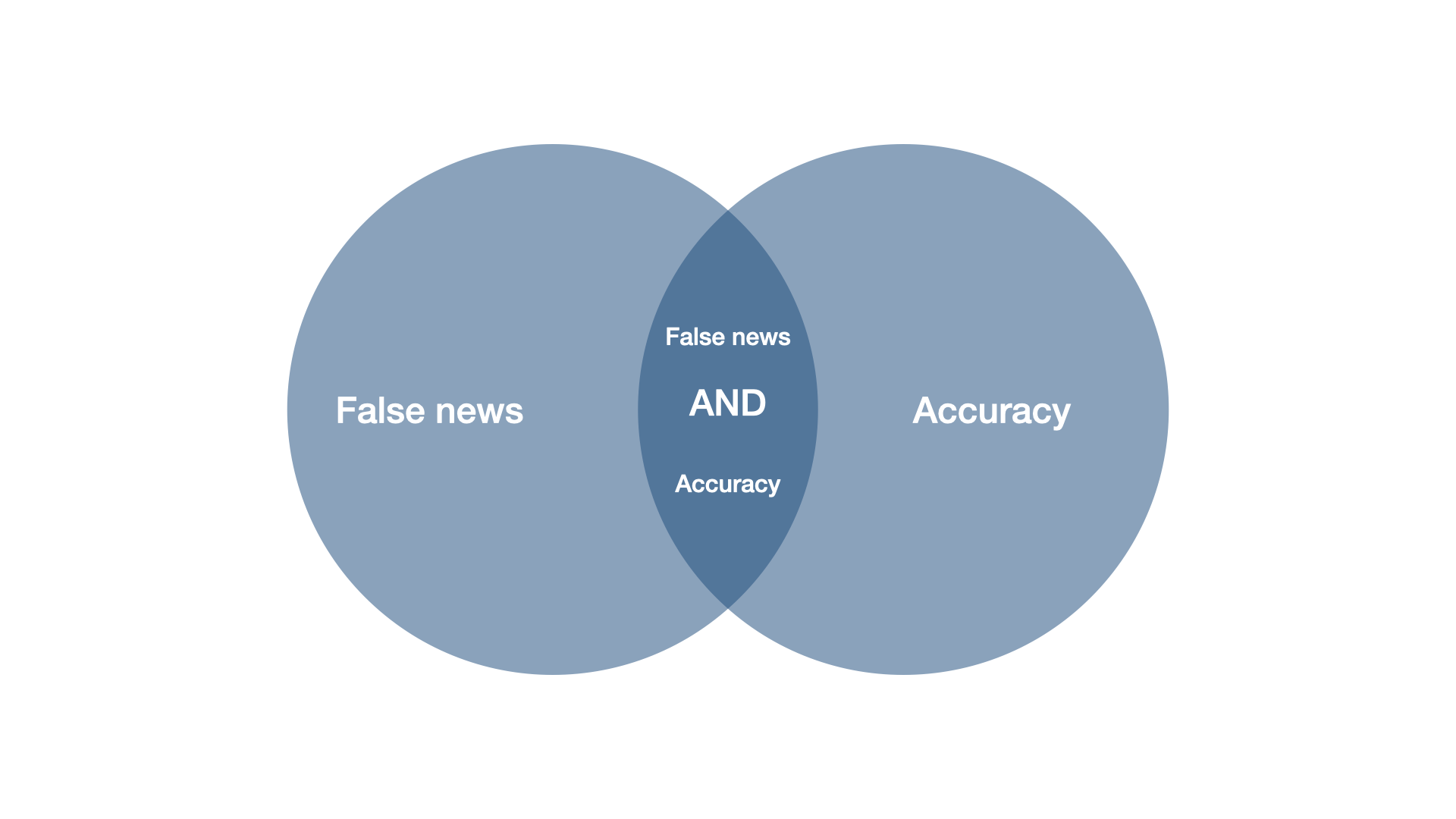
Boolean AND operator. Only if both keywords are included, a result will show up.

Boolean OR operator. As long as one of the keywords is included, a result will show up.

Boolean operators

‘“false news” OR “fake news” OR “false stor*” AND “accuracy” OR “discernment” OR “credibilit*” OR “belief” OR “susceptib*”’


Data bases

  • Google Scholar – great in most cases, but some disadvantages (e.g. user-specific results)


  • There are many other data bases out there:

    • Pubmed
    • Scopus
    • Web of Science
    • Your local university library catalogue
    • …

Data bases

Data bases allow very refined searches.

Data bases

Some databases also have features to export your search results as data sets.

Literature screening

There are several stages of deciding which studies to include:

  1. Title screening (sort out titles that are obviously irrelevant)
  2. Abstract screening
  3. Full-text screening

In particular in screening phases 2 and 3, all decisions are based on inclusion criteria (and must be documented!).

For example, some of our inclusion criteria were:

  • english language
  • a measure of accuracy for both true and false news
  • real-world news items only

PRISMA guidelines


  • The whole point of a systematic search is to have an exhaustive and unbiased pool of studies.

  • We won’t discuss the whole process here, but if you ever do a systematic review, you’ll want to check out the PRISMA guidelines for systematic reviews and meta-analyses

Running a meta-analysis

The meta-analytic average

  • A meta-analysis is basically taking an average of all effect sizes

Graphic adapted from: Harrer, M., Cuijpers, P., A, F. T., & Ebert, D. D. (2021). Doing Meta-Analysis With R: A Hands-On Guide (1st ed.). Chapman & Hall/CRC Press.

The meta-analytic average


…but not just a normal average - a weighted average.

  • The idea is that larger studies (with more participants/observations) are given more weight than smaller studies

  • This is typically done via the standard error of the effect sizes

Cohen’s d (part II): the standard error

Tip

Remember:

The standard error is a special standard deviation - the standard deviation of the sampling distribution (i.e. the–hypothetical–distribution of estimates we would expect from drawing many different samples from a population).

Cohen’s d (part II): the standard error


\[ SE_{\text{Cohen's d}} = \sqrt{ \frac{n_\text{true} + n_\text{false}}{n_\text{true} n_\text{false}} + \frac{d^2}{2(n_\text{true} + n_\text{false})} } \]

  • \(d\) = Cohen’s d
  • \(n_\text{false}\) = sample size of fake news items,
  • \(n_\text{true}\) = sample size of true news items,
  • and \(SD_{\text{pooled}}\) the pooled standard deviation of both groups (see above).

Tip

All you need to remember:

With greater sample size, smaller standard error (this should ring a bell from our class on statistical power).

Your turn:

Imagine you collected data from 9 studies

  1. Download the meta-analysis data meta_analysis_news.csv.

  2. Calculate Cohen’s d and its standard error (you can use this function which translates the previous formula into R code):

05:00

Solution

# Function to calculate pooled standard deviation
pooled_sd <- function(sd_true, sd_false) {
  sd_pooled <- sqrt((sd_true^2 + sd_false^2) / 2)
  return(sd_pooled)
}

# Function to calculate standard error of Cohen's d
se_cohen_d <- function(d, n1, n2) {
  se_d <- sqrt((n1 + n2) / (n1 * n2) + (d^2) / (2 * (n1 + n2)))
  return(se_d)
}

meta_summary <- meta_summary |> 
  mutate(pooled_sd = pooled_sd(sd_true, sd_fake), 
         cohen_d = discernment/pooled_sd, 
         se_cohen_d = se_cohen_d(cohen_d, n_ratings_true, n_ratings_fake)
         )

Calculate weigths


As noted earlier, the standard error helps us calculate a weight for each study \(k\) in our meta-analysis:

\[ w_k = \frac{1}{se^2_k} \]

  • \(se^2\) = squared standard error (also called variance) of a study \(k\)

Tip

Note:

The bigger the sample size, the smaller the standard error, the greater the weight.

Calculate the meta-analytic average


Based on the standardized effect sizes and their standard errors, we can finally calculate the meta-analytic average.

\[ \hat\theta = \frac{\sum^{K}_{k=1} \hat\theta_kw_k}{\sum^{K}_{k=1} w_k} \]

  • \(\hat\theta\) = estimate of the meta-analytic average

The meta-analytic average


In practice, you’ll always use existing R packages for these calculations.

There are many packages out there, but a popular one is the metafor package

Your turn:

Can people discern between true and false news? Use the metafor package and its rma.uni() function (check documentation by clicking on the function) to calculate the meta-analytic average.

Tip

  • you don’t need to specify the weights arguments

  • you only need to specify yi, sei and data

05:00

Solution

library(metafor)

meta_model <- rma.uni(yi = cohen_d, sei = se_cohen_d, data = meta_summary)

summary(meta_model)

Random-Effects Model (k = 8; tau^2 estimator: REML)

  logLik  deviance       AIC       BIC      AICc   
 -0.8852    1.7704    5.7704    5.6622    8.7704   

tau^2 (estimated amount of total heterogeneity): 0.0748 (SE = 0.0402)
tau (square root of estimated tau^2 value):      0.2735
I^2 (total heterogeneity / total variability):   99.79%
H^2 (total variability / sampling variability):  475.36

Test for Heterogeneity:
Q(df = 7) = 3115.1291, p-val < .0001

Model Results:

estimate      se    zval    pval   ci.lb   ci.ub      
  0.8318  0.0970  8.5780  <.0001  0.6418  1.0219  *** 

---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Forest plot

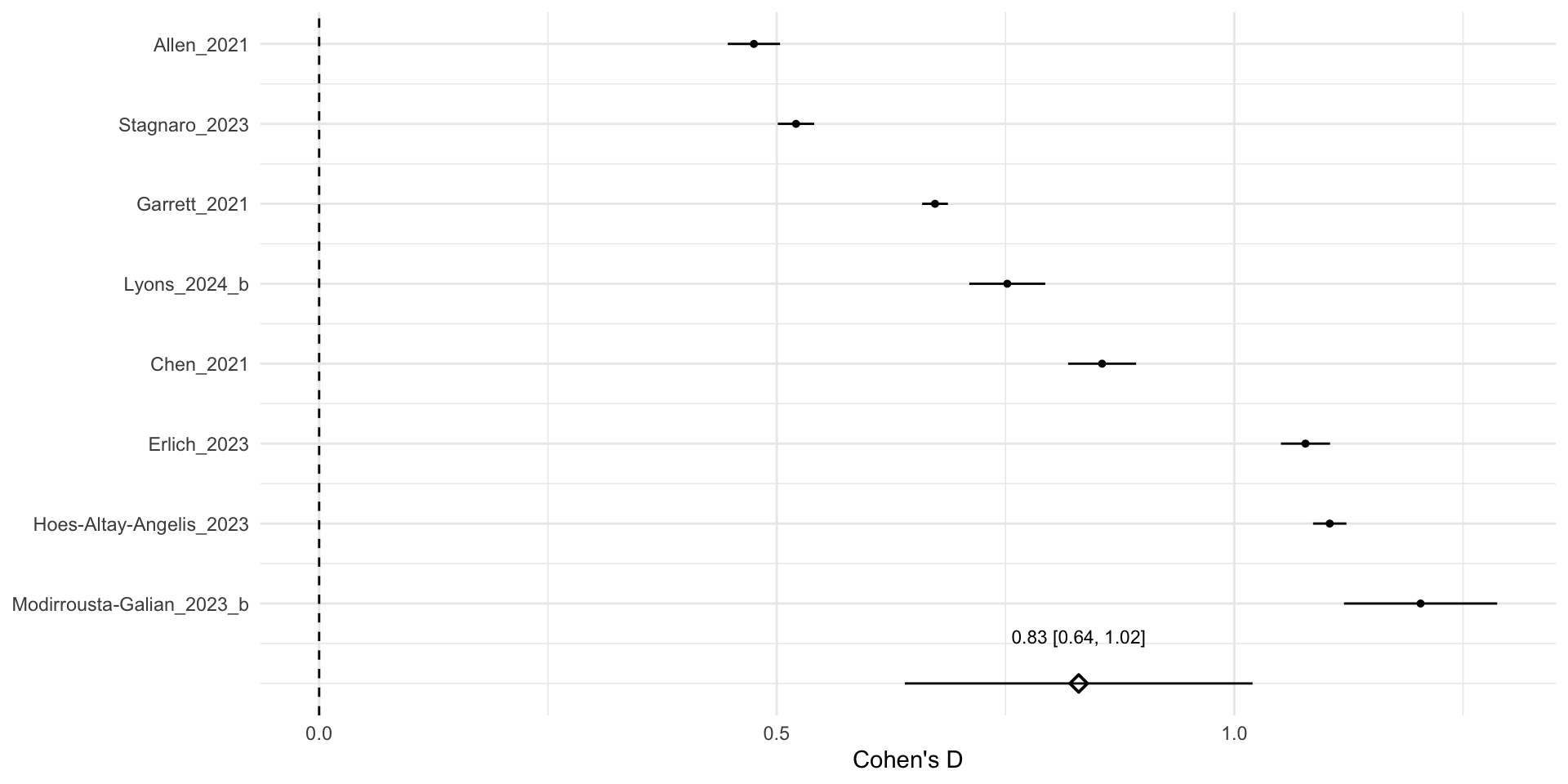
Points are effect sizes, bars are 95% confidence intervals - an indicator of statistical significance we haven’t discussed yet. The idea is that if they exclude 0, that’s like having a p-value below 0.05: the estimate is statistically significant.

Things we couldn’t cover (but you should know are possible)

  • There are many other standardized effect sizes for different variably types

  • We have only discussed fixed effects meta-analyses. Yet, for some research questions and data types, it is better to use slightly more complex, random effects meta-analyses

  • To test the effect of context factors, you can also run so called “meta-regressions”

  • Meta-analyses can reveal publication bias or p-hacking (see our class the replication crisis). Meta-analyses typically include several tests that can be indicative of this